Autor: Jesús Sánchez Rodríguez.
En una entrada anterior, Pequeño pero matón: breve introducción a la teoría de perturbaciones, nos preguntamos cómo podíamos obtener soluciones aproximadas a problemas donde no existía solución analítica. En un primer momento, utilizamos un caso conocido con solución analítica para ilustrar el procedimiento, el oscilador armónico amortiguado:
\begin{eqnarray}
\frac{d^2 x(t)}{d t^2} + 2 \varepsilon \frac{d x(t)}{d t} + x(t) = 0, \ \ \ \ \ \ \ \text{(1)}
\end{eqnarray}
donde $\varepsilon$ era un parámetro pequeño, es decir, $\varepsilon \ll 1$.
Sin embargo, cuando quisimos resolver este problema utilizando teoría de perturbaciones, nos percatamos de que la solución obtenida divergía debido a la aparición de términos seculares. Esto suponía un problema, pues si para un problema con solución analítica no podemos obtener una aproximación perturbativa aceptable, ¿cómo podemos conseguir una solución aproximada fiable para un problema más complicado?
El método que exponemos a continuación tiene en cuenta la existencia en el problema en cuestión de varias escalas de tiempo diferenciadas; por ejemplo, en el oscilador armónico amortiguado, se nos ocurren dos escalas muy diferentes: por un lado, el periodo de las oscilaciones y, por otro, el tiempo de decaimiento del sistema. Cuando se introduce una perturbación pequeña, este método suele fallar al describir correctamente la solución en tiempos largos, en particular durante el régimen transitorio. La perturbación induce generalmente una modulación lenta de la amplitud y/o de la fase. La uniformidad del desarrollo perturbativo se rompe debido a la no uniformidad de las distintas escalas de tiempo, lo que da lugar a la aparición de términos seculares y a la pérdida de validez de la aproximación. En efecto, la presencia de pequeñas perturbaciones activas durante un largo periodo de tiempo tiene un efecto acumulativo no despreciable. El método de múltiples escalas, que ahora introducimos, permite superar esta dificultad al incorporar explícitamente las escalas de tiempo rápidas y lentas que gobiernan la evolución del sistema. Este formalismo ya no considera al tiempo $t$ como la única variable relevante en la evolución del sistema, sino que introduce nuevas variables totalmente independientes entre sí, cada una de las cuales representa un tiempo característico del sistema que describe la evolución de fenómenos más lentos o más rápidos. Nos referiremos a estas nuevas variables como $t_0$, $t_1$, $t_2$, $\ldots$, $t_m$ y se definen con respecto al tiempo absoluto $t$ como $t_i = \varepsilon^{i} t $.
Veamos un ejemplo de aplicación del método utilizando el caso que nos atañe desde la entrada anterior, el problema (1). En un primer momento, vamos a utilizar dos escalas de tiempo: $t_0 = t$ y $t_1 = \varepsilon t$. Eso significa que nuestra expansión directa de la variable $x$ es, en este caso:
\begin{eqnarray}
x(t_0, t_1) = \sum_{i=0}^{\infty} \varepsilon^{i} x_i (t_0, t_1) = x_0(t_0, t_1)+\varepsilon x_1(t_0, t_1) + \varepsilon^2 x_2(t_0, t_1) + \cdots,
\nonumber
\end{eqnarray}
donde la dependencia con las dos nuevas escalas de tiempo aparece explícitamente en los argumentos de las variables. No obstante, no podemos introducir directamente esta expansión en la ecuación diferencial original, al no haber desarrollado las derivadas con respecto al tiempo absoluto $t$. Dado que ahora existen dos escalas de tiempo diferentes, derivar con respecto al tiempo producirá términos adicionales que entrarán como potencias de $\varepsilon$. De hecho, si expresamos la primera derivada utilizando la regla de la cadena tenemos:
\begin{eqnarray}
\frac{d}{dt} = \frac{\partial t}{\partial t_0} \frac{\partial t_0}{\partial t} + \frac{\partial t}{\partial t_1} \frac{\partial t_1}{\partial t} = \frac{\partial t}{\partial t_0} + \varepsilon \frac{\partial t}{\partial t_1},
\nonumber
\end{eqnarray}
y, escribiendo la segunda derivada en función de las nuevas escalas de tiempo:
\begin{eqnarray}
\frac{d^2}{dt^2} = \frac{d}{dt} \left( \frac{d}{dt} \right) = \frac{d}{dt} \left( \frac{\partial t}{\partial t_0} + \varepsilon \frac{\partial t}{\partial t_1} \right) = \frac{\partial^2}{\partial t_0^2} +2 \varepsilon \frac{\partial^2}{\partial t_0 \partial t_1} + \varepsilon^2 \frac{\partial^2}{\partial t_1^2},
\nonumber
\end{eqnarray}
donde se ha usado el teorema de Schwarz para establecer la igualdad de las derivadas cruzadas.
Ahora sí estamos en condiciones de reescribir el desarrollo perturbativo completo del problema, que en orden 0 y en orden $\varepsilon$ se escriben como:
\begin{align}
\mathrm{Orden}\, 0: \quad \frac{\partial^2 x_0(t_0, t_1)}{\partial t_0^2} + x_0(t_0, t_1) &= 0. \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \text{(2)} \\
\mathrm{Orden}\, \varepsilon: \quad \frac{\partial^2 x_1(t_0, t_1)}{\partial t_0^2} + x_1(t_0, t_1) &= -2 \frac{\partial^2 x_0 (t_0, t_1)}{\partial t_0 \partial t_1} -2 \frac{\partial x_0 (t_0, t_1)}{\partial t_0}. \ \ \ \ \ \ \ \text{(3)}
\end{align}
Es interesante notar que, a orden 0, la ecuación a resolver es idéntica que utilizando la expansión directa, salvo en su dependencia funcional, pues ahora aparecen escalas de tiempo adicionales. Resolver a orden 0 la ecuación (2) arroja:
\begin{eqnarray}
x_0 (t_0, t_1) = A(t_1) \cos t_0 + B(t_1) \sin t_0, \ \ \ \ \ \ \ \text{(4)}
\nonumber
\end{eqnarray}
donde $A$ y $B$ son constantes de integración que dependen de la escala temporal $t_1$ y no podemos determinarlas únicamente recurriendo a las condiciones iniciales del problema. Es necesario acudir al siguiente orden perturbativo para obtener expresiones directas para ambas amplitudes. Si introducimos la expresión de $x_0$ en (3):
\begin{eqnarray}
\frac{\partial^2 x_1(t_0, t_1)}{\partial t_0^2} + x_1(t_0, t_1) = 2 \sin (t_0) \left[ \frac{\partial A(t_1)}{\partial t_1} + A(t_1) \right] – 2 \cos (t_0) \left[ \frac{\partial B(t_1)}{\partial t_1} + B(t_1) \right],
\nonumber
\end{eqnarray}
obtenemos, en el lado izquierdo de la ecuación, la misma estructura que a orden 0; esto es, la ecuación del oscilador armónico pero para $x_1$. En el lado derecho, sin embargo, existe un término adicional que no obteníamos en la expansión directa, y que viene dado por las derivadas de $A$ y $B$.
Resolviendo la ecuación diferencial para $x_1$ volvemos a encontrar el mismo inconveniente que en la expansión directa: la aparición de términos seculares, originados por las soluciones particulares que aparecen cuando el sistema es forzado con la misma frecuencia que la frecuencia natural de oscilación del sistema. Sin embargo, ahora existe una manera de conseguir eliminar los elementos que producen términos seculares anulando el lado derecho de la ecuación. Esto lo conseguimos igualando a 0 los términos entre corchetes resolviendo el siguiente sistema de ecuaciones:
\begin{align}
\frac{\partial A(t_1)}{\partial t_1} + A(t_1) &= 0, \\
\frac{\partial B(t_1)}{\partial t_1} + B(t_1) &= 0,
\end{align}
cuya solución es $A(t_1) = a e^{-t_1}$ y $B(t_1) = b e^{-t_1}$, donde ahora $a$ y $b$ son constantes que no dependen de ninguna escala temporal y pueden ser obtenidas mediante las condiciones iniciales. Sustituyendo las expresiones de $A(t_1)$ y $B(t_1)$ en la ecuación (4) y usando como condiciones iniciales $x(0) = x_0$ y $x'(0) = x’_0$, la solución aproximada a primer orden puede escribirse como:
\begin{eqnarray}
x_0 (t_0, t_1) = x_0 e^{-t_1} \cos t_0 + x’_0 e^{-t_1} \sin t_0,
\nonumber
\end{eqnarray}
que finalmente expresamos en función de $t$ como:
\begin{eqnarray}
x (t) = x_0 e^{-\varepsilon t} \cos t + x’_0 e^{-\varepsilon t} \sin t. \ \ \ \ \ \ \ \text{(5)}
\end{eqnarray}
La potencia del método de múltiples escalas se plasma en la figura siguiente, donde se muestra la solución exacta del problema (1), la solución perturbativa obtenida mediante expansión directa (que ya vimos en una entrada anterior), y la solución que arroja el método de las múltiples escalas (5). De nuevo, las condiciones iniciales son $x(0)=1$ y $x'(0)=0$, y el valor del parámetro $\varepsilon$ es 0.1.
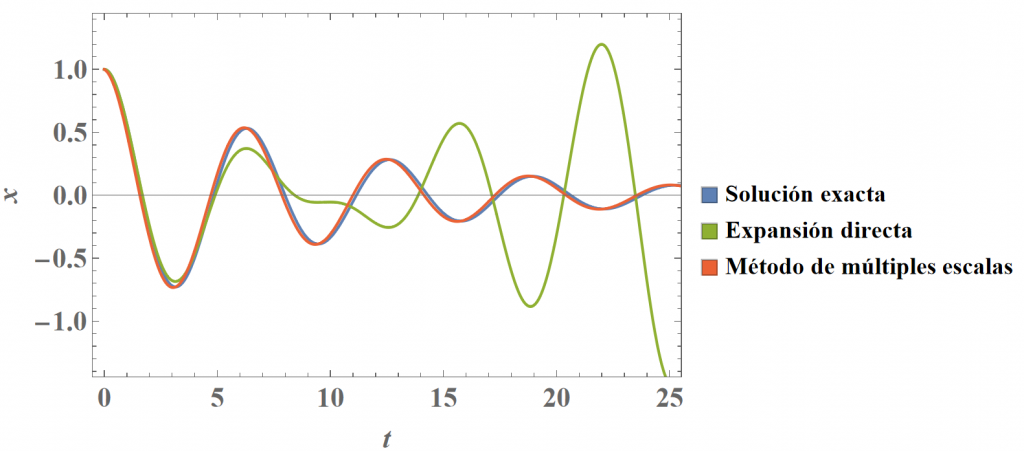
En este caso, la solución dada por el método de múltiples escalas (rojo) es casi idéntica a la solución exacta (azul), mostrando el decaimiento exponencial que la expansión directa (verde) no era capaz de exhibir. El método perturbativo que hemos presentado en esta entrada captura el comportamiento transitorio del sistema mediante la resolución de las ecuaciones de amplitud, algo que no aparecía en el caso de la straightforward expansion. La solución de múltiples escalas muestra la escala de tiempo correspondiente al periodo de las oscilaciones, de orden $\mathcal{O}(1)$, y la escala de tiempo correspondiente al decaimiento de la amplitud de las oscilaciones, de orden $\mathcal{O}(\varepsilon^{-1})$. De hecho, es posible ir más lejos y calcular la solución a segundo orden para descubrir otra escala temporal, $\mathcal{O}(\varepsilon^{-2})$, que corresponde a la variación temporal del ángulo de fase.
En definitiva, el método de las múltiples escalas es un método robusto, versátil y extremadamente útil para obtener soluciones aproximadas fiables de problemas complejos. En estas líneas hemos esbozado una aplicación muy específica del método de múltiples escalas, sin pensar en la generalización del método. Por ejemplo, para obtener la ecuación de amplitud hemos hecho uso de lo que conocemos sobre el oscilador armónico, es decir, que los términos proporcionales a $\sin(t_0)$ y $\cos(t_0)$ producen divergencias de la solución. Anulando estos términos hemos conseguido obtener las ecuaciones de amplitud. Una pregunta razonable sería plantearse qué ocurre si el miembro izquierdo que aparece en las ecuaciones (2) y (3) no es la ecuación del oscilador armónico. Entonces, ¿cómo encontramos las ecuaciones de amplitud que nos dan la solución del sistema?
Si esta entrada os ha parecido interesante, podéis encontrar mucha más información sobre los métodos perturbativos, en general, en esta excelente obra [1]. Además, para una introducción más amena al método de las múltiples escalas y otros aspectos de la teoría de sistemas dinámicos, os recomendamos este enlace [2], que forma parte de una serie de interesantísimos videos realizados por el Profesor S. Strogatz, de la Universidad de Cornell.
Autor: Jesús Sánchez Rodríguez.
Jesús Sánchez Rodríguez es investigador del Departamento de Física Aplicada II de la Universidad de Málaga.
Referencias:
[1] J. Kevorkian and J. D. Cole, Perturbation methods in applied mathematics, vol. 34.
Springer, New York, 1981.
[2] Steven Strogatz, 27 de abril de 2021. Lecture 22: Introduction to the method of multiple scales. Youtube. https://www.youtube.com/watch?v=kkN13nEn2WA.
