Autor: Adolfo Vázquez Quesada.

Cuando comenzamos el estudio de la dinámica en un curso de física general, la forma de proceder a la hora de resolver un problema es, en principio, bastante sistemática:

• Se elige un sistema de referencia.
• Se traza un diagrama de fuerzas
• En base al diagrama y con la segunda Ley de Newton en la mano, se plantean las ecuaciones de la dinámica que permitirán resolver el problema.

Por supuesto puede no ser tan fácil resolver el problema en cuestión, pues a veces, la elección de un buen sistema de referencia es importante para tener éxito, o puede que el sistema que manejemos esté a su vez acelerado y haya que tener en cuenta las fuerzas de inercia, o quizás el pérfido profesor haya incluido alguna dificultad extra. Pero, en principio, todos los problemas de dinámica que puedan aparecer durante el primer curso podrán ser dominados de esta manera. ¿Todos? ¡No! Hay un problema que se resiste cual pequeña aldea gala a la invasión romana: la polea. En realidad esto no es así, pero nadie lo diría viendo cómo la mayoría de los estudiantes resuelven los típicos problemas de poleas. Veamos dos de los esquemas que los alumnos usan más a menudo cuando se enfrentan a ellos:

1. Cuerpo unidimensional.

En este esquema, lo que se suele hacer es considerar los cuerpos de la polea y la propia cuerda como si formaran un único cuerpo unidimensional. En la siguiente figura se ve cómo es el sistema unidimensional equivalente:

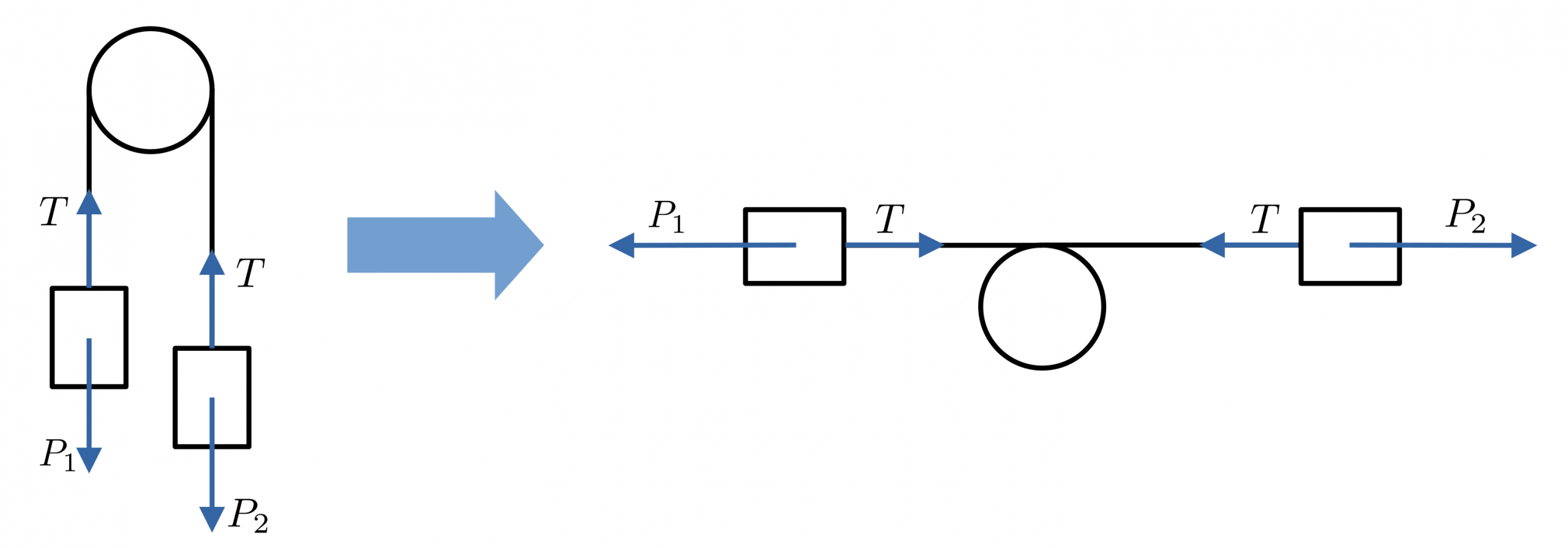
Los pesos de los cuerpos 1 y 2 se han denotado como $P_1$ y $P_2$ respectivamente, y la tensión de la cuerda como $T$. Si bien los alumnos que lo hacen así no dibujan el esquema de la derecha, cuando hablas con ellos queda claro que es este esquema equivalente el que tienen en mente. En este, se considera al sistema como un único cuerpo, de manera que las tensiones son fuerzas internas del cuerpo y no se tienen en cuenta. Al aplicar la segunda Ley de Newton en este sistema se obtiene
\begin{eqnarray} P_2 – P_1 = \left(m_1 + m_2\right)a. \end{eqnarray}
Nótese que como se considera un único cuerpo, la masa que se utiliza en el término de inercia (el de la derecha) es la suma de las masas de los cuerpos 1 y 2.

2. Siguiendo la cuerda

Diría que este es el esquema más utilizado. Se escribe una ecuación de fuerzas por cada cuerpo. Para determinar el sentido de las fuerzas, se elige una dirección de movimiento de la polea, y las fuerzas que siguen ese movimiento se toman como positivas y las que van en sentido contrario como negativas. Por ejemplo, en la siguiente figura, se ha elegido el sentido de movimiento hacia el lado del cuerpo 2, tal y como indica la flecha curva

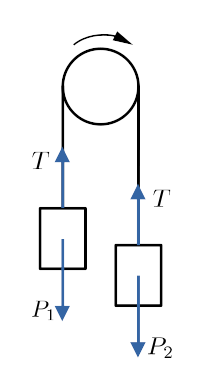
Así pues, siguiendo la cuerda las ecuaciones de las fuerzas para cada cuerpo son
\begin{eqnarray}
T – P_1 = m_1 a,
\nonumber\\
P_2 – T = m_2 a.
\nonumber
\end{eqnarray}
Si sumamos ambas ecuaciones, se obtiene la misma que en el esquema unidimensional
del primer punto:
\begin{eqnarray}
P_2 – P_1 = \left(m_1 + m_2\right)a.
\nonumber
\end{eqnarray}

Como vemos, ambos esquemas llevan al resultado correcto, pero no siguen los pasos habituales que se suelen utilizar para resolver los problemas de dinámica: en el primero hacemos una transformación del sistema a otro equivalente y en el segundo no definimos de forma explícita un sistema de referencia estandar. ¿Y qué tiene de especial la polea para que la gente no siga el esquema que sirve para todos los demás problemas? No lo tengo completamente claro, pero creo que es una cuestión de costumbre: si una mecánica de resolución funciona y es sencilla de seguir, no solemos cambiarla por otra mejor hasta que no aparece algo nuevo que no podamos resolver con nuestro esquema. Por esta razón, vamos a añadir un ingrediente más al problema que haga necesario sustituir dichas costumbres. En concreto, vamos a suponer que la polea tiene una aceleración $a_p$, tal y como se muestra en la siguiente figura:

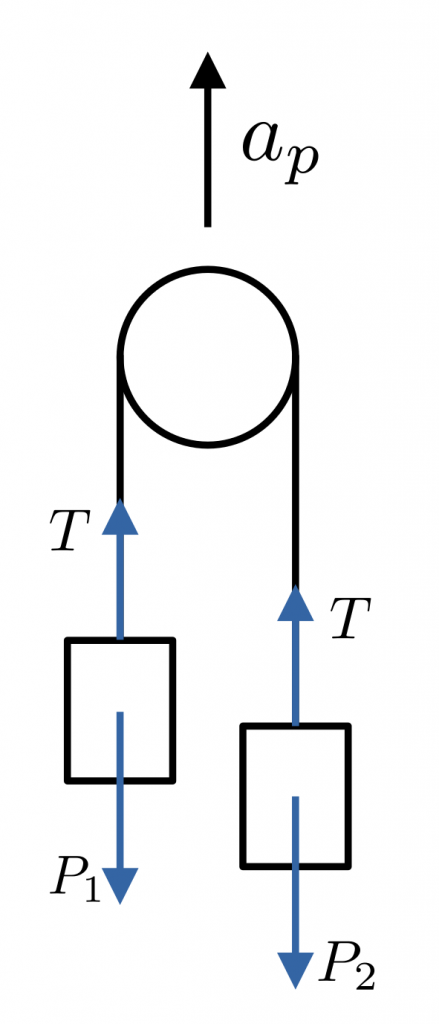
Esa aceleración puede venir, por ejemplo, de que, a su vez, la polea cuelgue de una cuerda que hace una fuerza hacia arriba. O si la polea pierde la sujeción y cae, sería la fuerza de la gravedad la que determinaría esa aceleración, que iría hacia abajo.

Si utilizamos el primer esquema, el del cuerpo unidimensional equivalente, tendríamos algo parecido a lo siguiente:

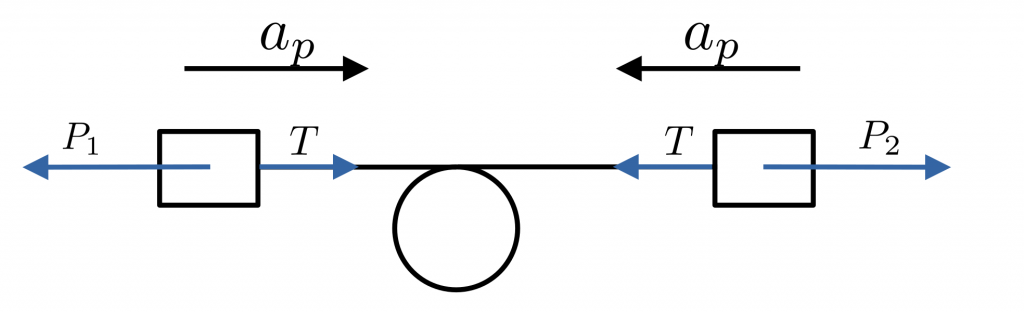
Vemos que la mitad del cuerpo sufriría esta aceleración hacia un lado, mientras que la otra mitad lo sufriría hacia el otro. No queda muy claro cómo resolver un problema en el que diferentes partes de un mismo cuerpo sufren diferente aceleración. Si fuéramos fieles a esta visión, llegaríamos a la conclusión de que las fuerzas asociadas a la aceleración $a_p$ no tienen ningún efecto, pues se anulan (la que va hacia la izquierda con la que va hacia la derecha), o que la cuerda no se va a mantener tensa, pues los cuerpos aceleran uno hacia el otro. Podemos adelantar que ninguna de estas cosas es correcta, por lo que en principio, no queda claro cómo incluir esta aceleración en las ecuaciones de Newton basándonos solo en dicho esquema.

Y si consideramos el segundo esquema, en el que seguimos la cuerda para definir los signos de las fuerzas, ¿cómo se abordaría una polea acelerada? Es verdad que entendiendo el problema en profundidad no es muy complicado incluir la aceleración en las ecuaciones, pero solo con este esquema en mente no es fácil estar seguro de cómo hacerlo, porque la aceleración $a_p$ de la polea no sigue la línea de la cuerda, por lo que no queda claro qué signo ponerle ni dónde, o al menos es lo que se deduce de los serios fallos que muchos estudiantes que siguen este esquema muestran cuando resuelven dicho problema.

¿Y cómo podemos entonces resolver un problema como este con garantías de que lo estamos haciendo correctamente? La forma más sencilla es seguir el mismo esquema que en cualquier otro problema de dinámica: se elige un sistema de referencia, se hace un diagrama de fuerzas y se aplica la segunda Ley de Newton. Comencemos por lo primero: el sistema de referencia. En la siguiente figura se indican el sistema de referencia que hemos elegido, así como el diagrama de fuerzas.

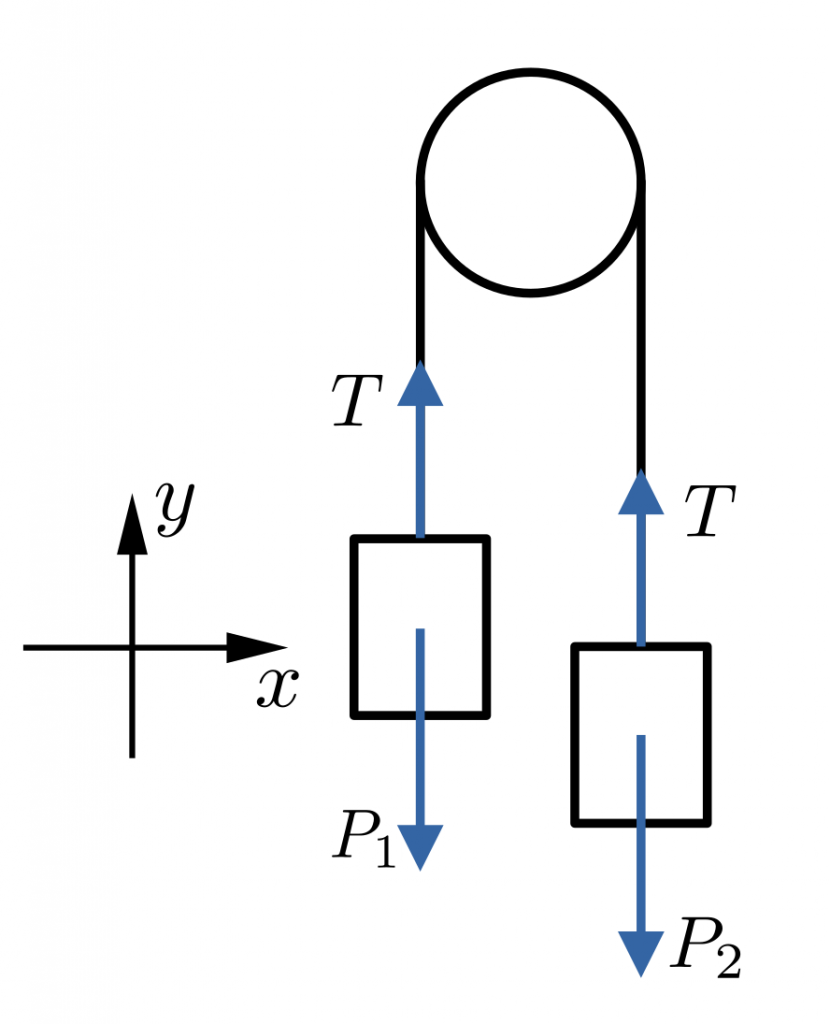
Por lo tanto, los vectores que vayan hacia arriba serán positivos, y los que vayan hacia abajo negativos. Si suponemos que la polea acelera hacia el cuerpo 2, las ecuaciones del sistema serán
\begin{eqnarray}
T-P_1 &=& m_1 a,
\nonumber\\
T-P_2 &=& -m_2 a,
\nonumber
\end{eqnarray}
que son equivalentes a las que obteníamos en los dos esquemas que vimos al principio. Pero ahora, cuando nos planteamos el problema de la polea acelerada, resulta mucho más natural introducir la aceleración $a_p$. Esto se hace como en cualquier otro problema con cuerpos que están en un sistema de referencia no inercial: añadiendo dicha aceleración a los términos de inercia (términos de la derecha). En este caso, el signo de $a_p$ queda muy claro con el sistema de referencia elegido, siendo positivo para ambos cuerpos (pues va hacia arriba). Las ecuaciones quedan
\begin{eqnarray}
T-P_1 &=& m_1 \left(a + a_p\right),
\nonumber\\
T-P_2 &=& m_2 \left(-a + a_p\right).\ \ \ \ \ \ \ \ \text{(1)}
\label{eqs_finales}
\end{eqnarray}
Nótese que los signos tomados en el caso en el que seguíamos la cuerda serían los mismos que los que obtendríamos suponiendo sistemas de referencia diferentes para cada cuerpo
como los indicados en la siguiente figura, lo cual nos da una pista sobre cómo incluir la aceleración $a_p$ en las ecuaciones obtenidas en ese caso.

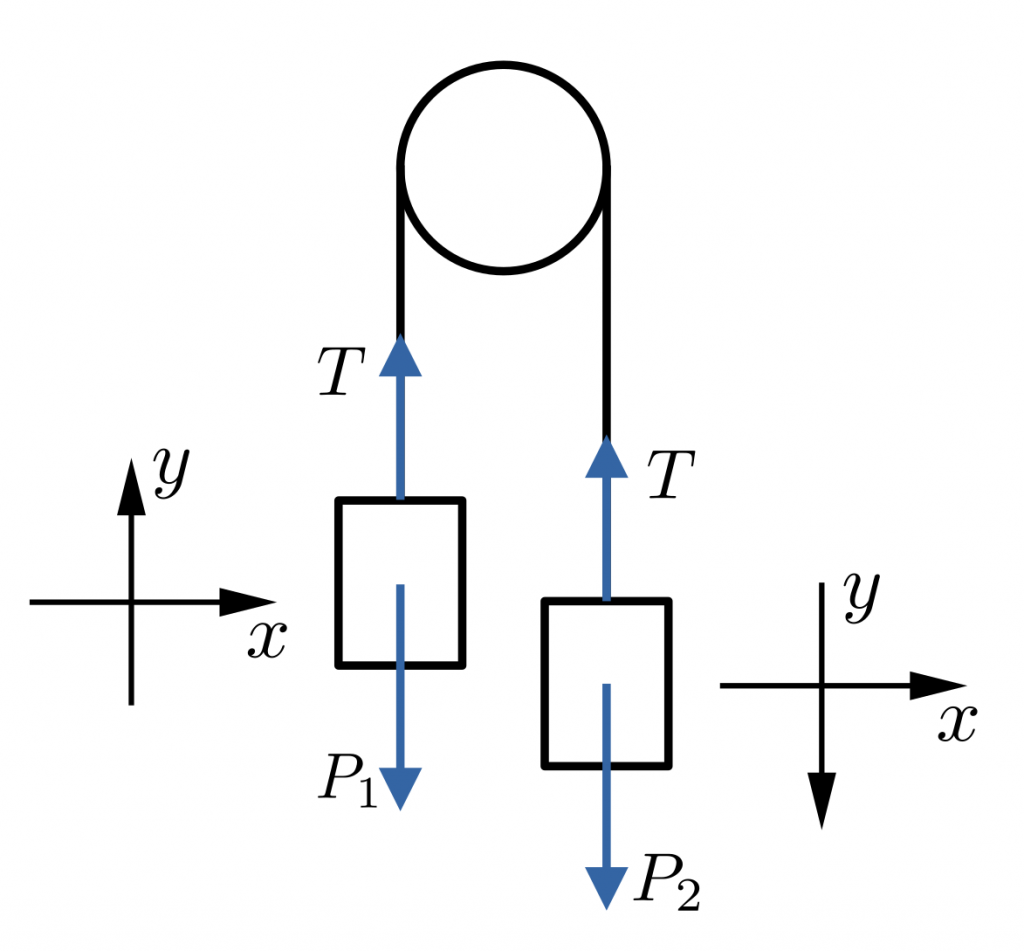
Merece la pena analizar un poco las ecuaciones (1) que hemos obtenido. Si restamos la segunda ecuación a la primera, se obtiene
\begin{eqnarray}
-P_1 + P_2 = m_1 \left(a + a_p\right) – m_2 \left(-a + a_p\right),
\nonumber
\end{eqnarray}
de donde deducimos la aceleración:
\begin{eqnarray}
a=\frac{\left(m_2 – m_1\right)}{\left(m_1 + m_2\right)}\left(g + a_p\right).
\nonumber
\end{eqnarray}
Si hacemos $a_p=0$ en esta ecuación, recuperamos la solución que se tendría si la polea no estuviera acelerada. También es importante darse cuenta de que si la polea cae libremente, entonces $a_p = -g$, que al sustituirlo en la ecuación anterior daría el resultado $a = 0$, por lo que los cuerpos 1 y 2 no se acelerarían respecto de la polea. Es decir, si inicialmente los cuerpos estuvieran en reposo respecto a la polea y esta de repente cayera por efecto de la gravedad, la polea junto con los cuerpos caerían como un todo. Por otro lado, si suponemos que la aceleración $a_p$ va hacia arriba, la aceleración de los cuerpos respecto de la polea será mayor cuanto mayor sea la aceleración $a_p$ de la polea.

Autor: Adolfo Vázquez Quesada.

Adolfo Vázquez Quesada es profesor del Departamento de Física Fundamental de la UNED.