Autor: Jesús Sánchez Rodríguez.

La descripción precisa de los fenómenos físicos pasa necesariamente por una modelización matemática. Esta modelización, más o menos adecuada o compleja, se plasma en todo tipo de ecuaciones a las que el físico debe enfrentarse para realizar su labor. En los estudios de Física estamos acostumbrados a resolver los problemas de manera analítica, esto es, encontrando una solución expresada mediante combinación de funciones conocidas y operaciones elementales. Sin embargo, la modelización de la naturaleza no siempre ocurre de esta forma y son innumerables los casos en los que las ecuaciones que representan los fenómenos físicos son irresolubles analíticamente. Una posibilidad ante este caso es resolver las ecuaciones de forma numérica. Otra, que es la que exploramos en esta entrada, es resolver las ecuaciones de forma aproximada bajo ciertas condiciones; por ejemplo, cuando existe un parámetro pequeño (mencionaremos qué significa pequeño más adelante) que modifica la estructura de una ecuación soluble analíticamente. En este caso, la solución de la ecuación se podrá escribir como la suma de la solución analítica de la ecuación sin el pequeño parámetro más una contribución que tiene en cuenta a éste (la perturbación). Este método, que constituye la llamada teoría de perturbaciones, es tremendamente eficaz en arrojar soluciones aproximadas de problemas no tratables analíticamente, permitiendo el análisis del sistema físico.

Existen varias técnicas dentro de la teoría de perturbaciones pero, para empezar, vamos a tratar el protocolo más sencillo. Asumamos, como hemos mencionado previamente, que la solución del problema puede descomponerse en dos partes: una solución correspondiente al problema analítico original, que sabemos resolver, y otra contribución, de menor importancia que la primera, que modula y tiene en cuenta las contribuciones que convierten al problema en irresoluble analíticamente. Matemáticamente, podríamos plasmar esta estrategia en un desarrollo en serie de potencias:

\begin{eqnarray}
x(t) = \sum_{i=0}^{\infty} \varepsilon^{i} x_i (t) = x_0(t)+\varepsilon x_1(t) + \varepsilon^2 x_2(t) + \cdots,
\nonumber
\end{eqnarray}

donde $x_0$ es la solución del problema sin perturbar y todos los términos con $\varepsilon$ aquellos que consideran la perturbación. El parámetro $\varepsilon$ es el parámetro «pequeño» que permite realizar el cálculo perturbativo o, mejor dicho, que asegura que la solución aproximada por este método sea lo más cercana posible a la solución real. Este método recibe el nombre de expansión directa o straightforward expansion.

Para comprobar la utilidad de este método perturbativo, apliquémoslo a un problema bien conocido con una solución exacta: el oscilador armónico amortiguado, representado por la siguiente ecuación diferencial

\begin{eqnarray}
\frac{d^2 X(T)}{d T^2} + 2 \xi \omega_0 \frac{d X(T)}{d T} + \omega_0^2 X(T) = 0,
\nonumber
\end{eqnarray}

con $\xi$ el coeficiente de amortiguamiento y $\omega_0$ la frecuencia natural de oscilación del sistema.

La obsesión constante de los físicos por el oscilador armónico perfectamente representada a través de esta figura (de la cuenta @mientrasenfisicas de X).

Podemos encontrar una escala de tiempo y longitud adecuadas de manera que la ecuación anterior, en unidades físicas, pueda expresarse de forma adimensional:

\begin{equation}
\frac{d^2 x(t)}{d t^2} + 2 \xi \frac{d x(t)}{d t} + x(t) = 0,\ \ \ \ \ \ \ \text{(1)}
\end{equation}

de manera que las variables en mayúscula representan variables dimensionales y las variables en minúscula adimensionales. No es difícil resolver esta ecuación, lo que nos va a permitir ver cómo de bueno es el método perturbativo: imaginemos que $\xi$ es una cantidad muy pequeña (gracias a escribir el sistema en su forma adimensional, pequeño implicará $\xi = \varepsilon \ll 1$), por lo que podemos desarrollar la solución de la ecuación como una parte sin perturbar y otra parte perturbada, únicamente a primer orden en $\varepsilon$, es decir, $x(t) = x_0(t) + \varepsilon x_1(t)$. Si introducimos este desarrollo en la ecuación anterior e igualamos por separado los términos con las mismas potencias de $\varepsilon$, tenemos:

\begin{align}
\mathrm{Orden}\, 0: \quad \frac{d^2 x_0(t)}{dt^2} + x_0(t) &= 0.\\
\mathrm{Orden}\, \varepsilon: \quad \frac{d^2 x_1(t)}{dt^2} + x_1(t) &= -2 \frac{dx_0 (t)}{dt}.
\end{align}

En el orden 0 del desarrollo perturbativo, observamos la ecuación del oscilador armónico, siendo $x_0(t) = A \sin(t+\phi) $, con $A$ y $\phi$ constantes determinadas por las condiciones iniciales. Cuando pasamos al siguiente orden, encontramos la ecuación de un oscilador armónico forzado:

\begin{eqnarray}
\frac{d^2 x_1(t)}{dt^2} + x_1(t) &= -2 A \cos(t+\phi).
\nonumber
\end{eqnarray}

Y aquí nos encontramos algo inesperado. La frecuencia de forzado es idéntica a la frecuencia natural de oscilación del oscilador, lo que conduce a un fenómeno bien conocido, la resonancia. Como este oscilador (no el sistema real, sino la ecuación que representa la contribución de primer orden) no tiene un término de amortiguamiento y, entonces, no disipa energía, el forzado a la frecuencia de resonancia conducirá irremediablemente a una divergencia, o «blow-up», de la solución para tiempos suficientemente largos. Ese «suficientemente largo» está íntimamente ligado al valor de $\varepsilon$. De hecho, esos términos que producen la divergencia de la solución son fácilmente calculables proponiendo una solución particular o mediante el método de variación de constantes; sin meternos en las cuentas, obtenemos que la solución particular tiene una contribución proporcional a $t \cos(t+\phi)$. Este término es el culpable de la divergencia de la serie perturbativa y recibe el nombre de término secular. De hecho, mostramos a continuación el gráfico de la solución de la ecuación (1) y de la solución perturbativa hasta primer orden.

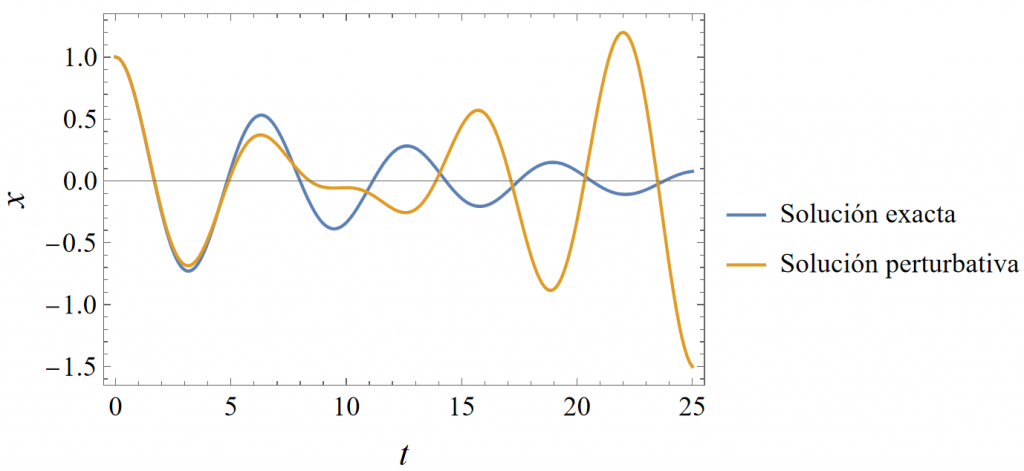
En esta figura, la solución exacta está representada en azul y la solución obtenida mediante cálculo perturbativo en naranja. Las condiciones iniciales son $x(0) =1$ y $x'(0)=0$ y el valor del parámetro $\xi=\varepsilon$ es $0.1$. Hasta $t \approx 5$ la solución perturbativa es bastante precisa, pero a partir de ese momento, ésta se aleja totalmente del comportamiento que el sistema exhibe. De hecho, poco después de $t\approx 10$, la solución perturbativa comienza a crecer de manera descontrolada y empieza a divergir, a causa de los términos seculares que ya hemos mencionado.

Pero, entonces, ¿para qué sirve esta expansión perturbativa si sólo nos da una solución aproximada válida para la primera parte de la trayectoria? En realidad esta expansión es bastante útil, solamente que no está especialmente adaptada para este sistema. ¿Se os ocurre qué puede estar pasando para que la aproximación no sea válida a tiempos «largos»? Por otro lado, ¿qué creéis que significa tiempos «largos»? En una próxima entrada trataremos de dar respuesta a la primera pregunta introduciendo otro método perturbativo que introduce una modificación bastante interesante de la straightforward expansion.

Autor: Jesús Sánchez Rodríguez.

Jesús Sánchez Rodríguez es investigador del Departamento de Física Aplicada II de la Universidad de Málaga.