Autor: José Manuel Moreno Valderrama.

Desde hace años, damos por supuesta la calidad visual de las producciones generadas por
ordenador, ya sean películas o videojuegos. Las sombras que proyectan los objetos, los reflejos en espejos o la sutil transferencia de color entre superficies cercanas, que vemos en cualquier fotograma de estas obras, podrían parecer a primer vista algo hecho a mano por artistas, como si un pintor hubiera pintado esos detalles. Nada más lejos de la realidad: la mayoría de estos efectos se generan a partir de ecuaciones complejas que describen cómo interactúa la luz con los distintos materiales. Es decir, cada fotograma es una simulación del comportamiento de la luz en el mundo real. Basta imaginar cómo la luz rebota en una mesa, toca la pared y luego se refleja en un espejo para intuir la enorme cantidad de matemáticas y física que intervienen en la escena.

El término técnico para lo descrito anteriormente es iluminación global. Su objetivo último es determinar el color que percibimos al mirar una escena bajo ciertas condiciones de iluminación. Resolverlo de manera exacta sería imposible, porque la luz rebota millones de veces entre superficies y cada interacción influye en el resultado final. Por eso se utilizan métodos aproximados que buscan reproducir este comportamiento de la forma más fiel posible a la realidad física.

Por si esto no fuera lo suficientemente difícil, muchas veces se necesita que estos cálculos se hagan muy rápido. Esto es lo que sucede en aplicaciones interactivas como los videojuegos, en los que cada frame debe servirse al usuario en alrededor de 16 milisegundos (60 frames cada segundo), lo que lleva en la mayoría de ocasiones a realizar aproximaciones menos realistas desde el punto de vista físico, pero igualmente convincentes visualmente.

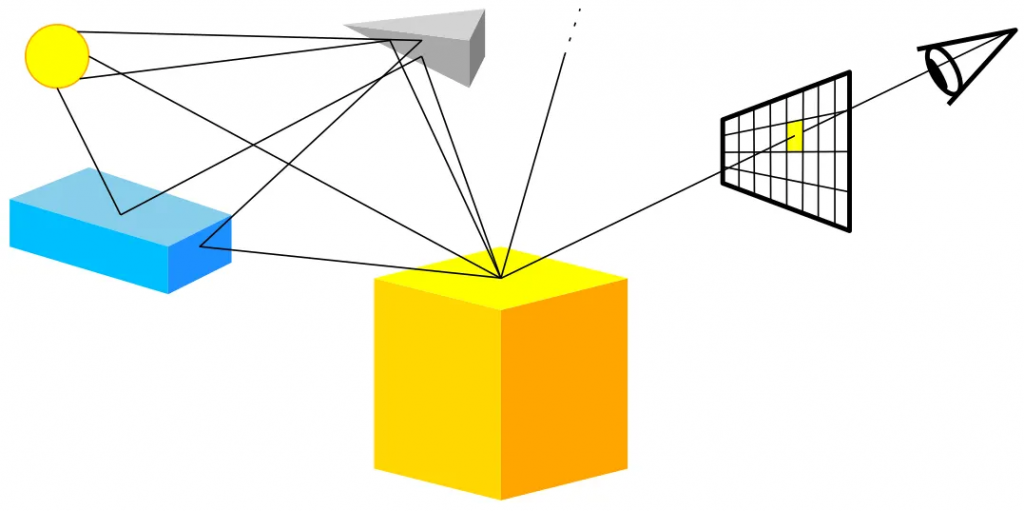
Para explorar cómo funcionan estos modelos, vamos a considerar una escena sencilla iluminada con una única fuente de luz muy lejana, como podría ser el Sol. Renderizar esta escena en una pantalla (esto es, producir una imagen a partir de ella) puede hacerse de varias maneras. En este caso optaremos por utilizar ray marching, una técnica de renderizado emparentada con el más conocido ray tracing.

De forma resumida, su funcionamiento puede entenderse así:

• Primero, creamos una cámara virtual. Cada píxel de la imagen que queremos generar tiene una posición en el espacio.
• Desde la posición de la cámara, lanzamos un rayo que pasa por cada píxel y lo dirigimos hacia la escena, avanzando en pasos discretos. Esto puede resultar sorprendente, ya que trazamos caminos desde el ojo hacia la escena, justo al contrario de lo que ocurriría en la realidad. Pero de esta manera exploramos únicamente los caminos que llegan a nuestros ojos.
• El avance del rayo podría hacerse con pasos de tamaño fijo, pero para optimizar los cálculos suelen emplearse las llamadas funciones de distancia con signo (SDFs).
• Estas funciones al ser evaluadas en un punto del espacio devuelven distancias a superficies definidas por ellas. Si tomamos el mínimo de todas esas distancias, obtenemos la distancia a la superficie más cercana en el mundo que hemos definido. Así, podemos avanzar en cada paso exactamente esa distancia sin miedo a chocarnos con nada. Si en algún momento, la función devuelve un valor cercano a cero, interpretamos que el rayo ha tocado una superficie.

Parar aclarar conceptos, en las siguientes imágenes puede verse un diagrama de una cámara virtual

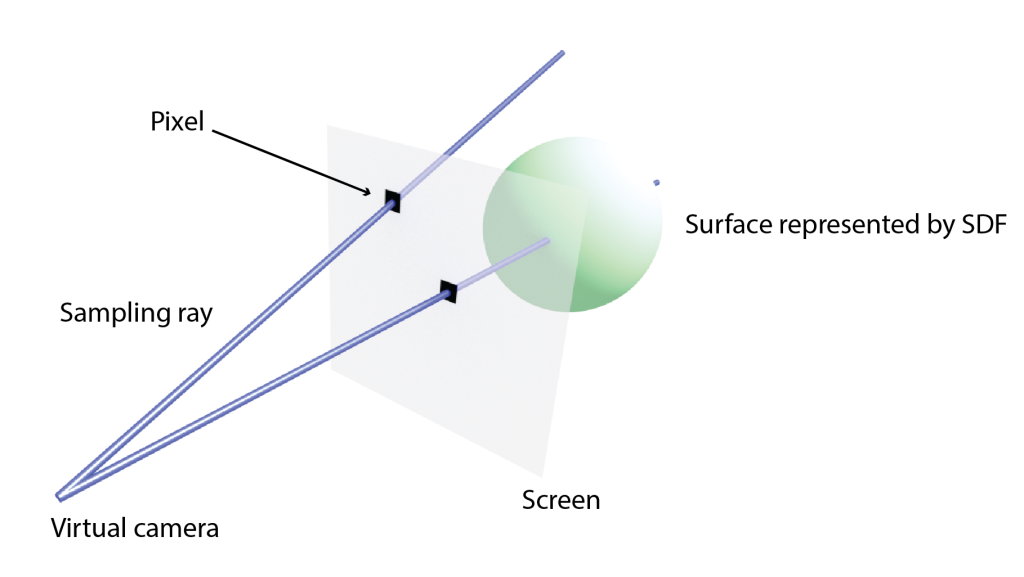
y del viaje de un rayo mediante la técnica de ray marching, en este caso una variante conocida como sphere tracing. Como hemos comentado antes, la distancia a la superficie más cercana determina exactamente cuánto podemos avanzar en cada paso.

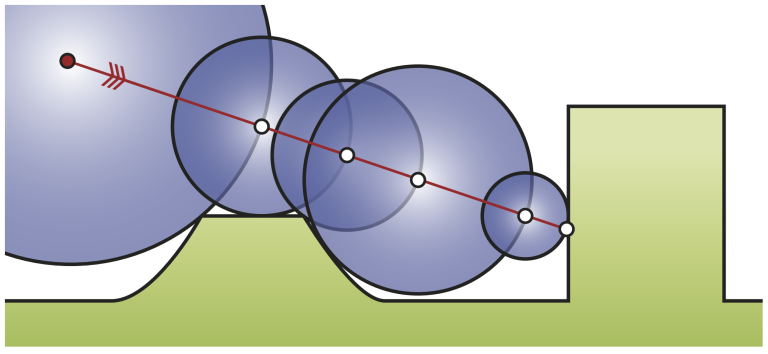
Un buen ejemplo de SDF sería la de una esfera centrada en el origen con un radio
determinado, que podría implementarse en GLSL (un lenguaje similar a C, ampliamente utilizado en programación gráfica) de la siguiente manera:

float sdSphere( vec3 pos, float rad ) { return length( pos ) - rad; }

Algo importante que aún no hemos mencionado sobre las SDFs es su signo. La función puede devolver un valor positivo o negativo, lo que nos indica si el punto está fuera o dentro de la superficie. Esta información puede resultar de gran utilidad según el caso que estemos tratando.

A continuación, podemos ver dos imágenes de nuestro ray marcher explorando una escena de prueba. Cuando choca con la superficie nos lo presenta con distintos colores:

• La normal de la superficie, en la primera imagen. El canal rojo del color representa la
  componente $x$ del vector normal, el verde la $y$, y el azul la $z$.
• La segunda es un poco más psicodélica, aunque se usa frecuentemente para obtener
  información de la escena. En este caso, estamos aplicando la función de dientes de sierra a cada dirección del espacio, y el resultado se codifica del mismo modo en los canales del color. Esto nos permite cubrir la escena con una serie de baldosas de tamaño unidad con información direccional.

Todos los ejemplos que vamos a ir exponiendo en el artículo han sido desarrollados con
Shadertoy, un entorno interactivo donde los shaders (programas escritos en GLSL) se ejecutan en tiempo real en la GPU del sistema. Cada shader define el color de cada píxel mostrado en pantalla. Al pie de cada figura incluiremos el enlace correspondiente al código, que puede consultarse, modificarse y ejecutarse libremente en la propia web.

El modelo Blinn-Phong

Este modelo empírico de iluminación, propuesto por Bùi T. Phong en su tesis en 1973 [2], y refinado posteriormente por James F. Blinn en 1977 [3], es considerado uno de los más influyentes en la generación de imágenes por ordenador (CGI).

El modelo establece que la intensidad total de la luz reflejada en un punto $P$ es la suma de tres componentes,

$I = I_a + I_d + I_s$,

donde $I_a$ representa la iluminacion ambiental, $I_d$ es la componente difusa, asociada a la luz dispersada uniformemente por la superficie, y $I_s$ es la componente especular, responsable de los reflejos característicos de materiales brillantes.

La iluminación ambiental es simplemente una constante, que evita la oscuridad absoluta en la escena. La componente difusa $I_d$ se calcula mediante la ley de Lambert que establece que la intensidad observada depende del coseno del ángulo entre la dirección de la luz $\boldsymbol{L}$ y la normal de la superficie $\boldsymbol{N}$, esto es,

$I_d = k_d\left(\boldsymbol{L}\cdot\boldsymbol{N}\right)I_L$,

donde $k_d$ es el coeficiente de reflexión difusa del material y $I_L$ la intensidad de la luz incidente.

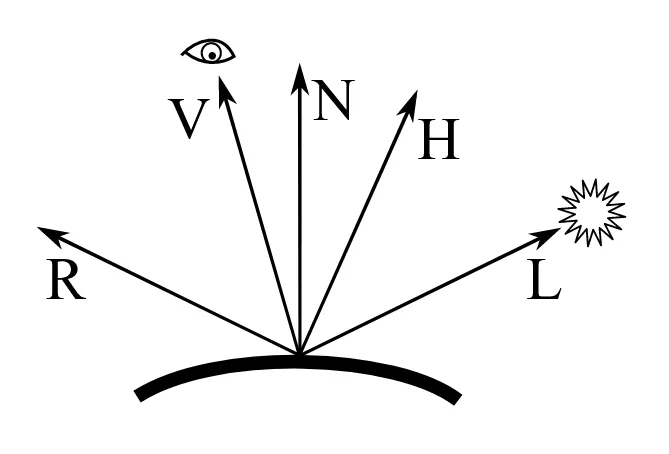
El término especular $I_s$ viene dado por,

$I_s = k_S\left(\boldsymbol{N}\cdot\boldsymbol{H}\right)^{n_s} I_L$,

donde $k_S$ es el coeficiente de reflexión especular del material, $n_s$ mide la concentración del brillo y $\boldsymbol{H}$ es el vector medio normalizado entre la dirección de la luz $\boldsymbol{L}$ y la dirección del observador respecto a la superficie $\boldsymbol{V}$,

$\boldsymbol{H} = \frac{\boldsymbol{L} + \boldsymbol{V}}{\left\arrowvert\left\arrowvert\boldsymbol{L} + \boldsymbol{V}\right\arrowvert\right\arrowvert}$.

Estas funciones tienen una implementación bastante directa en GLSL,

float ambient_term( float ka )
{
    return ka;
}

float diffuse_term( vec3 N, vec3 L, float kd )
{
    return kd * max( 0.0, dot( N, L ) );
}

float specular_term( vec3 N, vec3 L, vec3 V, float ks, float ns )
{
    vec3 H = normalize( L + V );
    return ks * pow( max( 0.0, dot( N, H ) ), ns );
}

Al elegir los colores de los objetos en nuestra escena, podemos crear algo similar a lo que se observa en la siguiente imagen. Las superficies iluminadas por nuestro sol virtual muestran un degradado que nos ayuda a intuir la posición de la luz. Además, la esfera refleja un brillo adicional que nos sugiere que estamos frente a una superficie reflectante. Este brillo especular depende de la posición del observador, a diferencia del componente difuso, que se mantiene constante desde cualquier ángulo.

Sin embargo, hay un detalle que no se ve del todo correcto: la luz ilumina zonas que deberían estar ocultas por otros objetos de la escena. En otras palabras, los objetos no proyectan sombras. Esto es completamente normal, ya que el modelo de Blinn-Phong, que estamos utilizando, solo tiene información del punto donde calculamos la luz. Dicho de otro modo, se trata de un modelo de primer orden, en cierto sentido.

Afortunadamente, la técnica de renderizado que hemos elegido, el ray marching, nos permite determinar si un objeto está tras otro o no. Pero tiene un coste: es necesario lanzar un rayo desde cada punto de la superficie hacia la fuente de luz. Si este rayo se encuentra con otro objeto en el camino, la superficie no debería recibir iluminación. Al aplicar esto, obtenemos la siguiente imagen, donde las sombras se proyectan correctamente y la escena se ve mucho más realista.

// Esto se ejecuta cuando el primer rayo que hemos lanzado ha chocado con alguna superficie.
// Tras ello lanzamos otro rayo hacia la luz, es decir, una rayo con 
// la dirección ldir, esto es, el vector L definido anteriormente.
// Los vectores nor y view son, respectivamente, N y V.
// Por último, sumamos las tres contribuciones, teniendo en cuenta la sombra.

float shadow = trace( ro + rd * hit.x+ 0.01 * nor, ldir ).x > 0.0 ? 0.0 : 1.0;
float Ia = ambient_term( 0.1 );
float Id = diffuse_term( nor, ldir, 1.0 );
float Is = specular_term( nor, ldir, view, 0.5, 100.0 );

col = ( Id * difcol + Is * specol ) * shadow + Ia * ambcol;        

La ecuación de renderizado

Aunque el modelo de Blinn-Phong es capaz de producir escenas visualmente estimulantes falla al intentar captar aspectos de la luz que percibimos cotidianamente. Es por ello, que con el paso del tiempo surgieron modelos con fundamentos físicos.

En este contexto, James T. Kajiya en el año 1986 presentó una ecuación para el transporte de la luz [4]

$L_0(\boldsymbol{x}, \omega_0, \lambda)=\int_\Omega f_r\left(\boldsymbol{x}, \omega_i, \omega_0, \lambda\right)L_i\left(\boldsymbol{x}, \omega_i, \lambda\right)\left(\boldsymbol{n}\cdot \omega_i\right)d\omega_i$,

que muestra cómo la radiancia reflejada $L_0$ de cierta longitud de onda $\lambda$ que refleja cierto objeto en una dirección $\omega_0$ es igual a una cierta suma ponderada sobre el hemisferio visible (definido por la normal de la superficie $\boldsymbol{n}$) de la radiancia incidente $L_i$ que llega de una cierta dirección $\omega_i$. Esta ecuación tiene como ingrediente principal la denominada función de distribución de reflectancia bidireccional $f_r$ o BRDF que especifica las propiedades de reflexión del material. Resumiendo: la luz reflejada por un objeto es la suma de la que le llega, modulada por su BRDF. En lo que sigue, tomaremos la BRDF igual para todas las longitudes de onda.

Una de las propiedades fundamentales de esta ecuación es que, siempre que la BRDF cumpla

$\int_\Omega f_r\left(\boldsymbol{x}, \omega_i, \omega_0, \lambda\right)\left(\boldsymbol{n}\cdot \omega_i\right)d\omega_i\le 1$,

tendremos una forma de conservación de la energía. Esta desigualdad nos indica que parte de la luz incidente es absorbida por el material y la reflejada no excede la que le llega.

Cabe mencionar que, en esta formulación, estamos dejando fuera fenómenos como la refracción de la luz al atravesar medios materiales, así como la emisión propia de los objetos, como la incandescencia o la luminiscencia. La ecuación de Kajiya se centra en el transporte y la reflexión de la luz incidente.

Entre las diversas BRDFs que modelizan el comportamiento de materiales tenemos la lambertiana, que es una función constante, definida por

$f_r\left(\boldsymbol{x}, \omega_i, \omega_0, \lambda\right) = \frac{\rho}{\pi}$,

válida para una idealización de un material que refleja la misma luz en todas las direcciones. El parámetro $\rho$ se denomina albedo difuso y va desde $0$ a $1$. Mide el cociente entre la luz reflejada y la luz incidente para una superficie dada. Introduciendo esta BRDF en la ecuación de renderizado obtenemos,

$L_0(\boldsymbol{x}, \omega_0, \lambda)=\int_\Omega \frac{\rho}{\pi}L_i\left(\boldsymbol{x}, \omega_i, \lambda\right)\left(\boldsymbol{n}\cdot \omega_i\right)d\omega_i$.

Para la resolución aproximada de esta ecuación suele usarse el método de Montecarlo, esto es, estimamos la integral evaluando múltiples direcciones y promediando sus contribuciones,

$L_0(\boldsymbol{x}, \omega_0, \lambda)\approx\frac{2\rho}{N}\sum_{n=1}^N L_i(\boldsymbol{x}, \omega_n, \lambda)\left(\boldsymbol{n}\cdot\omega_n\right)$.

La implementación de lo esbozado anteriormente, denominado path tracer, requiere de algunos cambios en nuestro ray marcher. En particular, requiere efectuar múltiples rebotes de la luz en la escena. La contribución a cada punto del espacio es extremedamente compleja. Por ejemplo, si tenemos un punto $\boldsymbol{x}_a$ , la luz puede haber llegado hasta él tras reflejarse previamente en otros puntos de la escena como $\boldsymbol{x}_b$ y $\boldsymbol{x}_c$ . En ese caso, pueden darse caminos como

• $\boldsymbol{x}_a \rightarrow \boldsymbol{x}_b \rightarrow$ fuente de luz
• $\boldsymbol{x}_a \rightarrow \boldsymbol{x}_c \rightarrow$ fuente de luz
• $\boldsymbol{x}_a \rightarrow\boldsymbol{x}_c \rightarrow \boldsymbol{x}_a \rightarrow$ fuente de luz
• $\boldsymbol{x}_a \rightarrow \boldsymbol{x}_b \rightarrow \boldsymbol{x}_a \rightarrow \boldsymbol{x}_b \rightarrow\boldsymbol{x}_c \rightarrow\boldsymbol{x}_a \rightarrow \ldots \rightarrow$ fuente de luz

Todos estos caminos contribuyen a la radiancia final que observamos en $\boldsymbol{x}_a$ . Por tanto, para programar un path tracer el proceso sería:

• Para cada píxel, generamos un camino (inverso) de luz, es decir, el recorrido que haría un fotón desde nuestro ojo hasta las fuentes de luz.
• El primer paso es encontrar el primer impacto (el último realmente) del fotón con una superficie de la escena.
• Desde ahí, se calcula una dirección aleatoria en el hemisferio visible y mandamos al fotón en esa dirección hasta el siguiente choque.
• En cada impacto, usamos la BRDF para acumular la luz reflejada y sumar su contribución a la radiancia final.
• Como es poco probable que un camino aleatorio llegue directamente a la fuente de luz, se aplican técnicas para acelerar la convergencia, por ejemplo, comprobar si cada punto está expuesto directamente a alguna fuente de luz. De este modo, se separan de forma natural las contribuciones directa e indirecta a la iluminación global dada por la integral.
• Para cada píxel, calculamos la radiancia de múltiples caminos y promediamos.

Una vez implementado y ajustando los parámetros adecuadamente podemos ver algo así. Lo primero que destaca al observar la imagen es que no hay bordes duros como nos pasaba en Blinn-Phong. La sombra, que era algo introducido ad-hoc en el anterior modelo, surge de una manera mucho más natural. Y, aunque muy sútil, podemos ver algo de transferencia de color de la esfera al suelo.

El siguiente fragmento de código calcula el color final del píxel.

// Para cada píxel formamos un camino de luz con varios rebotes.
for ( i = 0; i < bounces; i++ ) {
        vec2 res = trace( ro, rd );
        
        // Si nuestro rayo choca con algo, iniciamos el proceso de
        // de interacción de la luz con el material
        if ( res.x > 0.0 ) 
        
		        // Actualizamos la posición del rayo y calculamos
		        // el vector normal a la superficie.
            ro += rd * res.x;
            normal = computeNormal( ro ); 
            
            // Calculamos una nueva dirección en la hemiesfera visible. 
	          // Hemos omitido la lógica de rand_vector() para mejorar
	          // la lectura del código. Básicamente usamos un hash.
	          rand = rand_vector() - 0.5;
            rand *= sign( dot( rand, normal ) );
            
            // Esta dirección aleatoria se convierte en nuestra nueva dirección
            rd = normalize( rand );
            
            // Distinguimos entre los dos materiales de nuestra escena:
            // la esfera y el suelo. Acumulamos la contribución indirecta de la luz.
            float albedo = 1.0;
            if (res.y < 1.1)
						    luminance *= albedo * vec3( 1.0, 0.5, 0.2 );
						else if (res.y < 2.1)
						    luminance *= albedo * vec3( 0.75 );
            
            // Por seguridad, nos movemos un pelín hacia fuera de la superficie.
            ro += normal * 0.01;
            
            // Aqui lanzamos un rayo hacia la fuente de luzy acumulamos
            // la contribución directa de la luz.
            rand = rand_vector();
            vec2 reachsun = trace( ro, normalize( ldir + 0.2 * ( rand.xyz - 0.5 ) ) );
            float sunLight = dot( normal, ldir );
            if (sunLight> 0.0 && reachsun.y < 0.0 ) {
                direct += 2.0 * luminance * sunLight;
            }   
        }
        else
        {
		        // Terminamos ajustando el valor de radiancia final
		        // para mostrarlo adecuadamente en la pantalla.
		        col = 0.4 * ( direct + luminance );
            break;
        }
     }
     
     // Este color se acumula para cada frame y
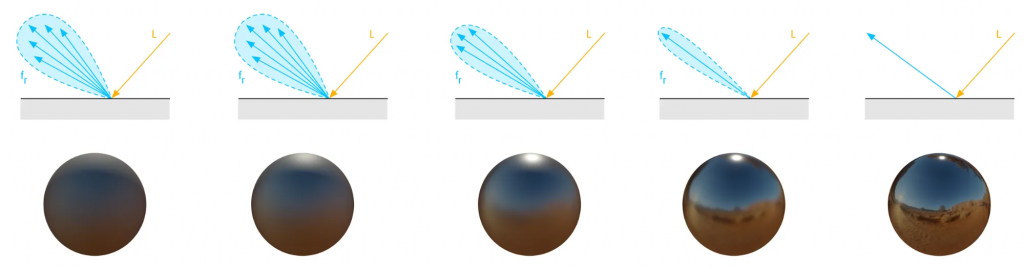
     // se promedia por los frames simulados.

Si en lugar de un material completamente lambertiano sesgamos el camino de salida de la luz, orientándola hacia la dirección del reflejo especular, obtenemos algo bastante interesante.

Ese pequeño cambio en la elección de las direcciones hace que la mayoría de los rayos reboten cerca del reflejo perfecto. El resultado es un material que empieza a mostrar brillos definidos, como si la superficie estuviera pulida o recubierta por una capa reflectante.

En términos más físicos, estamos modificando la distribución de probabilidad con la que muestreamos la hemiesfera: en lugar de hacerlo de forma uniforme (como en Lambert), favorecemos las direcciones donde el reflejo es más intenso. Esto es lo que hacen modelos como el de Cook-Torrance [5] o de microfacetas, que describen la superficie como una serie de pequeños espejos con distintas orientaciones.

En resumen: espero que con esta introducción el lector haya podido apreciar la cantidad de física que interviene en el problema de simular la luz. Pero no sólo eso: dentro del marco teórico que marca la física, también buscamos atajos, intentando equilibrar la precisión de los modelos con la calidad percibida en la obra final. En el fondo, renderizar es encontrar ese punto intermedio entre lo que la física dicta y lo que nuestros ojos aceptan como real.

Autor: José Manuel Moreno Valderrama.

José Manuel Moreno Valderrama es licenciado en Matemáticas y tiene un máster por la Universidad Autónoma de Madrid. También es graduado en Física por la UNED. Actualmente trabaja en Remedy Entertainment como Senior Technical Artist.

Referencias

[1] Korndörfer, B. K. H. S. J., Stamminger, U. G. M., & Keinert, B. (2014). Enhanced sphere tracing. STAG: Smart Tools & Apps for Graphics, 8(4), 1-8.

[2] Bùi T. Phong (1973). Illumination for computer-generated images. Thesis.

[3] Blinn, J. F. (1977). Models of light reflection for computer synthesized pictures. In Proceedings of the 4th annual conference on Computer graphics and interactive techniques (pp. 192-198).

[4] Kajiya, J. T. (1986). The rendering equation. In Proceedings of the 13th annual conference on Computer graphics and interactive techniques (pp. 143-150).

[5] Cook, R. L., & Torrance, K. E. (1982). A reflectance model for computer graphics. ACM Transactions on Graphics (ToG), 1(1), 7-24.