Autor: César Antonio Carvajal de la Haza.
¿Alguna vez te has parado a pensar en las redes que nos rodean? Desde el mapa del metro hasta la compleja estructura de tus contactos en una red social, todos son grafos: nodos (estaciones, personas) conectados por enlaces (líneas de metro, amistades). Estas representaciones, que nos acompañan en el día a día, son una herramienta matemática poderosa que nos permite modelar sistemas complejos en campos tan diversos como la ingeniería o la biología.
Pero, ¿qué sucede si llevamos esta idea al fascinante mundo de la física cuántica?
Imagina que esos nodos ahora son sitios cuánticos donde pueden habitar partículas. Las conexiones entre ellos representarían las interacciones físicas que les permiten moverse o saltar de un sitio a otro. Podemos describir estas interacciones mediante una matriz de adyacencia, que nos dice dónde están las conexiones físicas. Por ejemplo, imagina un sistema con 4 sitios conectados en línea: 1 − 2 − 3 − 4. Este grafo físico puede representarse mediante una matriz de adyacencia, donde cada fila y columna corresponde a un nodo del sistema (la primera a 1, la segunda a 2, y así sucesivamente). La matriz refleja las conexiones físicas entre los nodos: un 1 indica que dos nodos están conectados y un 0 que no lo están.

Ahora bien, en mecánica cuántica, existe un fenómeno que desafía nuestra intuición clásica: el entrelazamiento. Es una correlación tan fuerte y no local entre partes de un sistema que no tiene análogo en el mundo macroscópico. Piensa en ello como una conexión invisible que va más allá de los enlaces físicos evidentes, algo así como una ruta oculta en el mapa del metro. Dos sitios cuánticos podrían no estar directamente conectados en nuestro grafo físico original, pero aún así compartir una gran cantidad de información cuántica simplemente por estar entrelazados.
Aquí es donde surge la pregunta más intrigante: ¿podría este entrelazamiento cuántico generar su propia red entre los nodos? ¿Una especie de grafo cuántico emergente que quizás no se parezca en nada al grafo original de las conexiones físicas?
Esta es la cuestión que abordé en mi trabajo de fin de grado en Física, defendido el curso pasado. Junto a mi tutor, exploré la relación entre las conexiones físicas de un sistema y su estructura de entrelazamiento. El objetivo era determinar hasta qué punto ambas geometrías —la física y la cuántica— se parecen… o no. Para ello, consideramos un modelo simple, pero representativo: un conjunto de sitios cuánticos donde habitan bosones duros, es decir, partículas que no pueden compartir el mismo sitio. Estas partículas pueden saltar de un sitio a otro cuando existe una conexión física entre ellos, lo que se conoce como interacción de hopping. La estructura del sistema queda entonces definida por un grafo, donde los enlaces indican qué sitios están conectados y permiten dichos saltos.
En la siguiente figura se muestra un ejemplo: hay tres bosones —representados por esferas de Bloch— que pueden moverse libremente entre los distintos sitios, siempre que estos no estén ocupados.
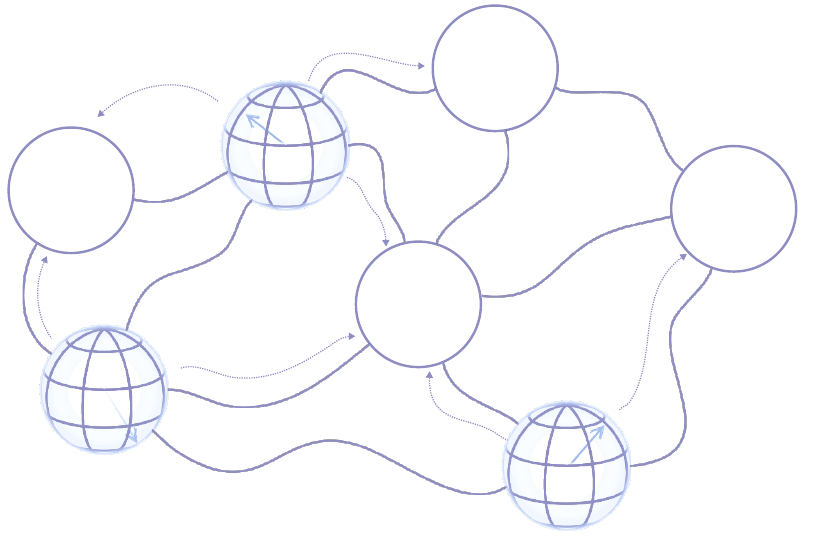
entre sí tienen una línea que los une. Los bosones pueden moverse a sitios que no estén ocupados y que estén conectados entre sí. Se indican con flechas los movimientos posibles.
En la figura hemos dibujado solo una configuración de las muchas posibles, cuya cantidad está dada por el número combinatorio $C_{7,3}$, siempre respetando la regla de que no puede haber más de uno en cada nodo. Ahora bien, en lugar de analizar cada configuración de forma aislada, la mecánica cuántica nos ofrece una herramienta mucho más elegante: todas las diferentes posibilidades pueden reunirse en un único objeto matemático que describe cómo se relacionan entre sí y cómo evoluciona el sistema. Ese objeto es el Hamiltoniano, la matriz que condensa toda la física del problema. A partir de él podemos calcular cuál es el estado fundamental del sistema, es decir, el estado de mínima energía. El procedimiento detallado lo veremos más adelante –no desesperen–. Por ahora basta con quedarse con la idea de que en esa matriz está codificada toda la información esencial.
La ley del área del entrelazamiento
¿Y qué nos dice ese estado cuántico sobre la estructura interna del sistema? Aquí es donde entra en juego la llamada ley del área del entrelazamiento, que conecta la geometría con la mecánica cuántica. Esta ley afirma que el entrelazamiento entre una región del sistema y el resto escala con el tamaño de la frontera entre ambas [1]. En otras palabras: si dividimos el sistema en dos grupos de sitios, la cantidad de entrelazamiento entre ambos grupos no depende del tamaño de cada grupo, sino del número de enlaces que atraviesan la división. Si la interacción es local, es decir, sólo conecta nodos vecinos, entonce el entrelazamiento también tiende a serlo.

Pese a haberla llamado una ley, no siempre se verifica. Hay sistemas físicos para los que el grafo asociado al entrelazamiento no coincide con el definido por las interacciones del Hamiltoniano. Desafortunadamente, aún no se comprende bien cuáles son los sistemas para los que dicha violación se verifica. Dicho conocimiento sería muy útil tanto desde el punto de vista fundamental como desde el aplicado.
Veamos entonces cómo extraer el grafo asociado al entrelazamiento del estado fundamental de nuestro Hamiltoniano. La herramienta clave se conoce como matriz de adyacencia del entrelazamiento (MAE) [2,3], que describe las correlaciones cuánticas entre los diferentes nodos. La MAE asigna un número a cada par de sitios, que indica la cantidad de entrelazamiento que existe entre ellos. Una matriz de adyacencia siempre nos dice quién está conectado con quién, y la MAE nos dice quién está entrelazado con quién. Así podremos comparar la red física, definida por las interacciones del Hamiltoniano, y la red cuántica, revelada por la MAE. ¿Coinciden siempre? Si se cumple la ley del área del entrelazamiento, así será.
Procedimiento matemático
Esta sección es un poco más técnica, y puede saltarse en una primera lectura.
- En primer lugar elegimos el grafo de las interacciones físicas y escribimos el llamado Hamiltoniano de Hubbard para $N/2$ partículas en $N$ sitios. Escribimos la lista de todas las configuraciones del sistema, es decir, todas las formas de elegir $N/2$ sitios ocupados de entre los $N$, que vienen dadas por el número combinatorio $N_T=C_{N,N/2}$. Ahora escribimos una matriz $N_T\times N_T$, en el que la configuración $I$ y la $J$ estarán conectadas si existe una forma de llegar de una a la otra moviendo una única partícula a lo largo del grafo.
- Diagonalizamos dicha matriz numéricamente y nos quedamos con el estado fundamental, que llamaremos $|\Psi\rangle$. Obtenemos la matriz densidad asociada, $\rho=|\Psi\rangle\langle\Psi|$.
- Para cada pareja de sitios, $i$ y $j$, obtenemos la matriz densidad reducida asociada a la pareja, y a cada uno de los sitios individuales, $\rho_A=\text{Tr}_{\bar A}\rho$, donde $A=\{i\}$, $\{j\}$ y $\{i,j\}$.
- Obtenemos las entropías de entrelazamiento asociadas a las tres matrices, $S_i$, $S_j$ y $S_{ij}$, que se obtienen desde sus autovalores $\lambda_k$ a través de $S=-\sum_k \lambda_k \log\lambda_k$.
- La entrada de la matriz de adyacencia será $M_{ij}={1\over 2}(S_i+S_j-S_{ij})$.
La figura siguiente ilustra el procedimiento.

Un ejemplo sencillo: la cadena periódica
Para empezar, consideraremos un caso sencillo: una cadena de 8 sitios conectados de forma periódica, es decir, donde el primer y el último sitio también están conectados, formando un anillo. Cada sitio puede albergar un bosón, y los bosones pueden saltar de un sitio a otro según las reglas dictadas por el Hamiltoniano del sistema. Tendremos 4 bosones que viven en esos 8 sitios.

Los resultados obtenidos se representan en forma de matriz. Por un lado, tenemos la matriz de adyacencia del grafo físico, que simplemente nos dice qué sitios están conectados por las interacciones del sistema. Por otro lado, construimos la MAE, que recoge cuánto entrelazamiento cuántico existe entre cada par de sitios. Ambas matrices tienen la misma forma —una tabla de 8 × 8 en este caso—, pero reflejan aspectos muy distintos: la primera está dictada por la estructura del Hamiltoniano (quién puede saltar a dónde), mientras que la segunda surge del análisis del estado fundamental del sistema (quién está realmente correlacionado con quién). Compararlas nos permite ver hasta qué punto el entrelazamiento respeta la geometría del sistema, o si, por el contrario, emergen patrones inesperados.

Para facilitar la interpretación visual, a la derecha de la MAE se incluye una barra de color que indica la intensidad del entrelazamiento entre cada par de sitios. No se muestran los valores numéricos exactos: solo se marcan los extremos —mínimo y máximo—, ya que lo importante aquí no es el número en sí, sino el patrón de conexiones que revela el entrelazamiento.
En el ejemplo de la cadena lineal se puede observar que ambas matrices son similares. Esto apoya sin duda la ley del área. Sin embargo, no ocurre así en todos los casos.
Explorando otras geometrías
Después de analizar el caso de la cadena lineal periódica, podemos preguntarnos qué ocurre si consideramos otras geometrías. ¿Cómo afecta eso al entrelazamiento cuántico? ¿Sigue respetándose la ley del área o emergen patrones distintos?
En esta sección exploramos otras configuraciones de conexiones físicas —más complejas o menos regulares— para comprender cómo se comporta la red de entrelazamiento. Comparar las MAE obtenidas nos permite entender mejor la relación entre la forma del sistema y su estructura cuántica interna. Veamos primero la que hemos bautizado como geometría puente:
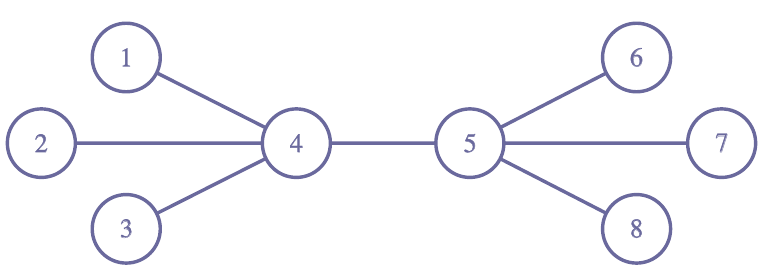
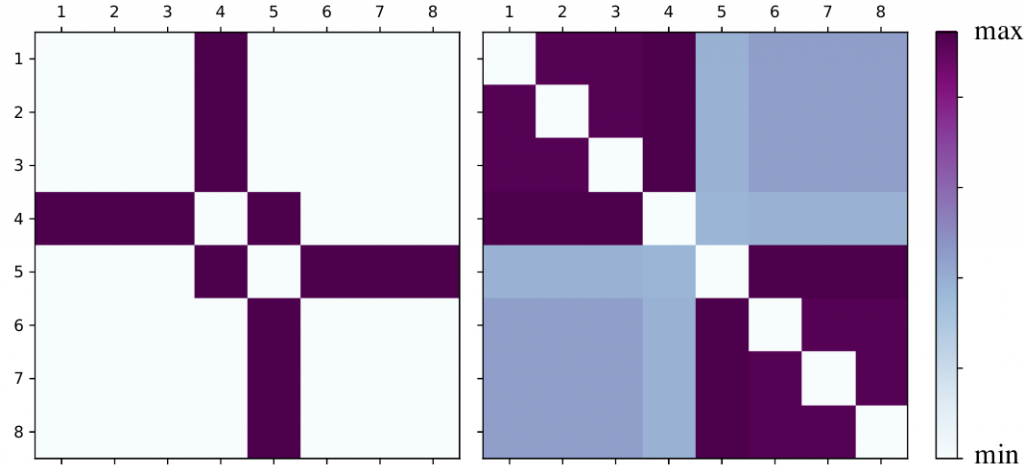
Los resultados que se obtienen con esta geometría son especialmente reveladores:
- El puente que conecta los sitios 4 y 5, lejos de reforzar el entrelazamiento, aparece sorprendentemente débil. Esto sugiere un posible efecto de desentrelazamiento local, quizá por competencia con otros enlaces.
- En cambio, los sitios 1, 2 y 3, que originalmente no estaban directamente conectados, muestran ahora una fuerte correlación cuántica entre ellos.
- También aparecen nuevos enlaces entre sitios alejados, como el 1 y el 6, que en la geometría original no mostraban relación alguna.
Vemos así los primeros indicios de una separación clara entre la matriz de adyacencia física y la MAE: aunque comparten estructura formal, pueden reflejar relaciones muy distintas entre los sitios del sistema. Esta diferencia no es casual. Esto se puede entender a la luz de la llamada monogamia del entrelazamiento: a diferencia de las correlaciones clásicas, el entrelazamiento no puede compartirse libremente. Si dos sitios están fuertemente entrelazados entre sí, no pueden estar igualmente entrelazados con otros. Esto explica por qué, en ciertos casos, el entrelazamiento se redistribuye y aparece en lugares inesperados. Es como si el entrelazamiento fuera un recurso limitado: cuando se gasta mucho entre dos sitios, queda menos para el resto.
Pasamos a ver otro ejemplo, la que hemos bautizado como geometría árbol:

Esta geometría, jerárquica y con una estructura de ramificación clara, introduce una topología no muy distinta a la anterior. En este caso, se tienen 13 sitios con 6 bosones. A través del estudio de la MAE, podemos comentar lo siguiente:
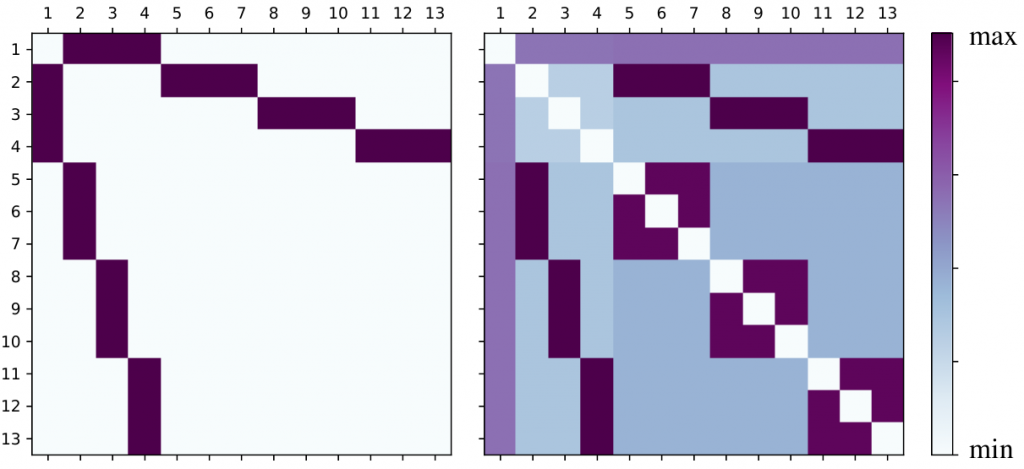
- El nodo raíz (1) adquiere relevancia en la MAE, pese a estar conectado a tres nodos en la matriz de adyacencia. La razón es que su entrelazamiento se distribuye entre muchos nodos, especialmente al llegar a niveles más profundos. Es como si llegase a conectar con todos.
- La estructura hace que la distribución del entrelazamiento favorezca las hojas (nodos terminales), que acumulan más correlación que los nodos intermedios. Esta tendencia es consistente con lo observado en la geometría puente. Esto es, las posiciones más externas (como 5, 6, 7) muestran entrelazamientos fuertes entre sí, a pesar de no estar directamente conectados.
- La geometría árbol muestra una tendencia a empujar el entrelazamiento hacia los extremos del sistema, en línea con lo observado en la geometría puente, donde los enlaces más internos se debilitan y los extremos tienden a entrelazarse más intensamente. Esto puede interpretarse como una forma en que el sistema busca optimizar el entrelazamiento entre zonas poco conectadas, al no poder concentrarlo en los nodos centrales debido a restricciones de monogamia.
A modo de cierre
A lo largo de este recorrido hemos visto que el entrelazamiento cuántico no es solo un concepto muy intrigante de la mecánica cuántica, sino una herramienta poderosa para entender cómo se organizan dichos sistemas. Incluso en modelos sencillos —como partículas que saltan entre sitios— pueden surgir estructuras internas sorprendentes, que revelan relaciones ocultas más allá de la geometría física del sistema. Conceptos como la ley del área del entrelazamiento, la monogamia cuántica o la construcción de la matriz de adyacencia del entrelazamiento nos ofrecen una nueva mirada: no solo sobre lo que está conectado, sino sobre lo que realmente está correlacionado.
El objetivo de este trabajo ha sido analizar la relación entre la geometría de interacción y la distribución del entrelazamiento en un sistema de bosones duros. A través de distintos ejemplos, hemos explorado cómo el entrelazamiento se reparte en el sistema y hasta qué punto sigue —o no— la conocida ley del área, revelando que la geometría cuántica no siempre refleja de forma evidente las conexiones físicas originales.
Para aquellos interesados en seguir profundizando, las referencias incluyen artículos sobre la MAE y sobre el papel del entrelazamiento como geometría emergente, así como textos más generales que abordan la física de sistemas cuánticos correlacionados.
Además, todo el código utilizado para realizar las simulaciones de este trabajo se encuentra disponible en mi repositorio de GitHub: Enlace aquí.
Autor: César Antonio Carvajal de la Haza.
César Antonio Carvajal de la Haza, es graduado en Física por la UNED.
Referencias
[1] J. Eisert, M. Cramer, M.B. Plenio. Colloquium: Area laws for the entanglement entropy, Reviews of Modern Physics, 82, 277 (2010).
[2] S. Singha Roy, S.N. Santalla, J. Rodríguez-Laguna, G. Sierra. Entanglement as geometry and flow. Phys. Rev. B 101, 195134 (2020).
[3] S. Singha Roy, S.N. Santalla, G. Sierra, J. Rodríguez-Laguna. Link representation of the entanglement entropies for all bipartitions. Journal of Physics A: Mathematical and Theoretical, 54, 305301 (2021).

Muy buena entrada. Y es la primera en el blog sobre el trabajo realizado en un TFG. Gracias César por compartirlo. 🙂
Hola, Adolfo. Muchas gracias por tu comentario 🙂 Ha sido todo un placer escribir la entrada, así que me alegra leer tu opinión. Aprovecho también para agradecer a mi tutor, Javier, por proponerme escribirla y por acompañarme a lo largo de todo el trabajo.