Autor: Jesús Sánchez Rodríguez.

En una entrada anterior nos interesamos sobre los distintos regímenes de caída que exhibían los objetos cuando se les dejaba caer a merced de la gravedad. Para recordar, el sistema físico era el siguiente: un objeto altamente simétrico y con una dimensión mucho mayor que las otras dos dimensiones características del objeto. Si hablamos de un paralelepípedo, por ejemplo, buscamos uno cuya longitud sea muy superior al espesor y anchura del cuerpo. Además, dicho objeto se encontraba totalmente sumergido en un fluido cualquiera. Dejábamos caer este objeto con una posición inicial dada y una velocidad inicial nula, tras lo cual observábamos la trayectoria que el cuerpo describía para poder categorizarla en los cuatro regímenes generales que encontramos: steady descent, fluttering, tumbling y chaos.

Una vez hemos recordado el problema, podemos volver a la última pregunta que planteábamos en la primera parte de la entrada. Nos gustaría saber, antes de que el objeto caiga, cuál será su régimen de caída atendiendo únicamente a las características físicas del flujo y también geométricas del sólido. Está claro que el fluido donde se encuentra el objeto tiene que ser importante; no es lo mismo dejar caer una hoja de papel en el aire que en el agua. Pero el cuerpo que consideremos también reviste importancia: hoja de papel y piedra no caen de la misma forma en el aire. Lo que no sabemos, a priori, es la importancia relativa de una característica u otra. Ni tampoco si hay alguna variable más que no hayamos considerado previamente pero que pueda influenciar el régimen de caída. Tratemos de responder primero a esta última cuestión usando el análisis dimensional. Un objeto de densidad $\rho_s$ y de longitudes características $L$ (longitud), $w$ (anchura) y $t$ (espesor) cae sometido a la aceleración de la gravedad $g$ en un fluido de densidad $\rho_f$ y viscosidad cinemática $\nu$. Pongamos también, para ser un poco más generales, que las dimensiones del objeto son desiguales y que se cumple la desigualdad $L \gg w > t$. Como la dimensión $L$ del objeto es muy superior a las otras dos, podemos plantear el problema físico prescindiendo de ésta y asumir un comportamiento bidimensional. Tenemos en total 6 variables físicas ($\rho_s$, $w$, $t$, $\rho_f$, $\nu$, $g$) y, si indagamos sobre las dimensiones de estas variables, veremos que estas dimensiones representan únicamente a 3 magnitudes físicas: masa, longitud y tiempo. Podremos afirmar entonces que existen tres grupos de variables adimensionales que describen la caída del objeto. Esta aseveración es profunda y tiene una enorme importancia física. Podemos tratar de deducir sin hacer ni un solo experimento de qué grupos adimensionales podría depender la caída del cuerpo; también podemos equivocarnos y no elegir los parámetros más relevantes, pero una discusión completa sobre este tema (análisis dimensional y teorema de Buckingham $\pi$) bien merece una entrada aparte. Volviendo al tema, los grupos adimensionales que podemos formar y que se utilizan tradicionalmente para describir este fenómeno son:

\begin{eqnarray}
\mathrm{AR}= \displaystyle\frac{t}{w}, \qquad I^{*} = \displaystyle\frac{I}{\pi \rho_f w^4/32}, \qquad \mathrm{Re}= \displaystyle\frac{U w}{\nu}.
\nonumber
\end{eqnarray}

Estos parámetros son la razón de aspecto entre la dos longitudes $\mathrm{AR}$, el momento de inercia adimensional $I^{*}$ y el número de Reynolds $\mathrm{Re}$. La razón de aspecto únicamente toma en cuenta el cociente de las dos longitudes, siendo un parámetro generalmente pequeño en los experimentos $(\mathrm{AR}< 0.1-0.2)$ y que suele considerarse de poca o nula influencia en la determinación del régimen de caída. Esta afirmación, ampliamente aceptada, es, sin embargo, cuestionada y refutada parcialmente en algunos trabajos computacionales [1]. El momento de inercia adimensional se define como el momento de inercia del sólido que cae normalizado por un momento de inercia de referencia. A saber, el momento de inercia por unidad de longitud con respecto al eje de simetría de un cilindro de fluido de densidad $\rho_f$ y diámetro $w$. Otros estudios toman como parámetro adimensional el cociente entre densidades de objeto y fluido, aunque se opta por el momento de inercia adimensional por razones históricas [2, 3]. Por último, el número de Reynolds, que toma para su definición una velocidad característica $U$ de caída, la cual suele tomarse en el experimento como la velocidad media de caída del objeto. Esta decisión, sin embargo, entraña un serio problema: el número de Reynolds no es un parámetro a priori, sino a posteriori. Es decir, es necesario realizar el experimento para medir la velocidad con la que el objeto cae para formar el Reynolds, lo que complica tomar $\mathrm{Re}$ como parámetro de control. No obstante, este parámetro se elige tradicionalmente porque permite la comparación de los nuevos experimentos realizados en este campo con la ingente cantidad de datos experimentales que se llevan obteniendo desde el pasado siglo [2-4]. Sin embargo, otros autores han propuesto cambiar este parámetro por otro realmente de control que no necesite del experimento para cuantificarse. En concreto, se suele tomar el número de Arquímedes, $U_g w/\nu$, [1] (también llamado de Galileo, según la referencia) que toma como velocidad característica la velocidad de caída del objeto $U_g$ obtenida igualando las tres fuerzas predominantes que aparecen en la Figura 1. Estas fuerzas (tomadas por unidad de longitud $L$) son el peso, el empuje y el arrastre. Esta última es proporcional al cuadrado de la velocidad porque el número de Reynolds suele ser relativamente elevado, lejos, por tanto, de un flujo de Stokes. El balance de fuerzas $\mathrm{Empuje} + \mathrm{Arrastre} = \mathrm{Peso}$ nos permite escribir la velocidad de caída como:

\begin{eqnarray}
\rho_f w t g +\frac{1}{2}\rho_f w U_g^2 = \rho_s w t g \Longrightarrow U_g= \sqrt{2\left( \frac{\rho_s}{\rho_f} – 1 \right) t g } .
\nonumber
\end{eqnarray}

Por lo tanto, los parámetros que tomaremos determinantes en la elección de los distintos regímenes de caída son el momento de inercia adimensional y el número de Reynolds. Encontrar la dependencia de estos regímenes de caída con respecto a los parámetros adimensionales $I^{*}$ y $\mathrm{Re}$ se ha llevado a cabo teórica, numérica y experimentalmente. Los acercamientos teóricos se han basado principalmente en desarrollar modelos fenomenológicos utilizando la segunda ley de Newton. Numéricamente, el procedimiento es computacionalmente costoso pero permite variar la geometría del objeto y los parámetros físicos del fluido de manera sencilla, así como obtener resultados próximos a la realidad. Existen sendas referencias donde este problema es enfrentado teórica y numéricamente. El tratamiento experimental resulta especialmente interesante porque es el marco que los trabajos teóricos y computacionales tratan de racionalizar. Además, ha sido ampliamente desarrollado debido a la relativa simplicidad de la configuración experimental: un recipiente amplio relleno de fluido (aire, agua o glicerol son los empleados con más frecuencia), un dispositivo automático de soltado del objeto, distintas geometrías que dejar caer y una cámara para filmar la trayectoria. La representación de estos datos se plasma en los llamados diagramas de fase, gráficos bidimensionales que muestran el régimen de caída de los objetos en función de sus valores de inercia adimensional y número de Reynolds. En los gráficos, los distintos comportamientos están separados los unos de los otros mediante fronteras trazadas con líneas. En la Figura 2 se pueden observar dos diagramas de fase para dos tipos de objetos diferentes: la Figura 2 a) muestra los datos de Smith [2] para placas, mientras que la Figura 2 b) representa los datos de Field et al. [4] para discos delgados.

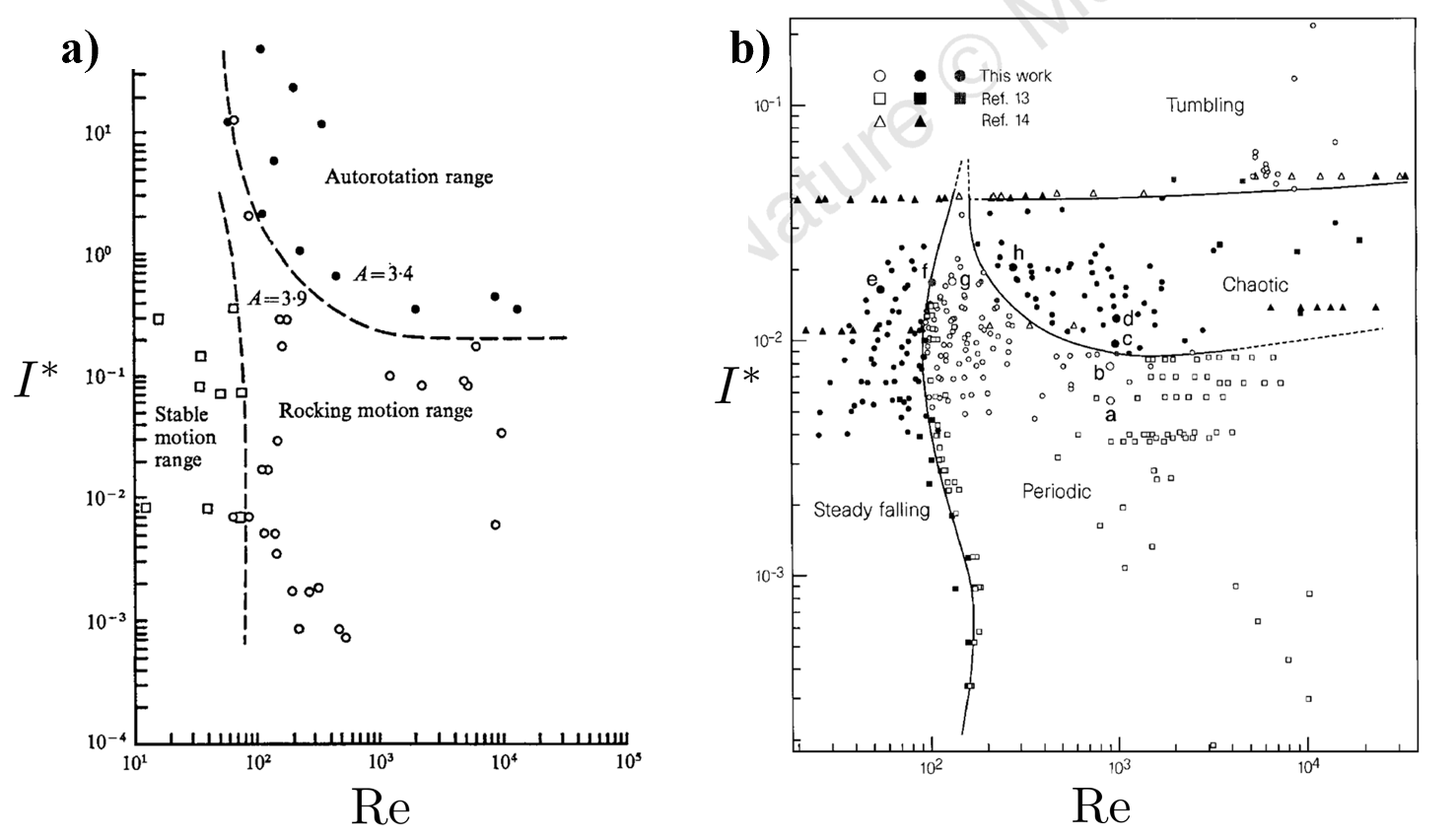
Ambos diagramas muestran los comportamientos que comentamos en la entrada anterior. El movimiento de steady descent, stable motion range para las placas y steady falling para los discos, se encuentra a valores bajos de números de Reynolds $(\mathrm{Re} \lessapprox 100)$ y valores bajos a moderados de inercia. El movimiento de fluttering (rocking motion range / periodic) se extiende a elevados números de Reynolds y mantiene los valores de inercia para los que se encontraba steady descent. El comportamiento de tumbling (autorotation) se observa sistemáticamente para moderados y elevados números de Reynolds e inercias elevadas. Es interesante notar que Smith no encuentra un comportamiento caótico en la caída de sus placas, a diferencia de Field, que localiza esta región entre el movimiento de fluttering y tumbling. Resulta sorprendente, además, que para otros experimentos realizados con placas delgadas se encuentren movimientos caóticos [6], lo que podría indicar que hay una fuerte dependencia del caos con las condiciones experimentales. Grosso modo, los dos diagramas de fase, aunque traten de objetos geométricos distintos, son cualitativamente muy similares.

Podríamos preguntarnos qué pasaría si tratásemos de incluir en el diagrama de fases la razón de aspecto, por ejemplo. O considerar objetos de geometrías más desafiantes. Incluso añadir otras características que objetos reales posean tales como porosidad o flexibilidad. Como veis, existen varias vías con las que continuar y obtener, posiblemente, resultados muy inspiradores.

Autor: Jesús Sánchez Rodríguez.

Jesús Sánchez Rodríguez es investigador del Departamento de Física Aplicada II de la Universidad de Málaga.

[1] Auguste, F., Magnaudet, J., & Fabre, D. (2013). Falling styles of disks. Journal of Fluid Mechanics, 719, 388-405.

[2] Smith, E. H. (1971). Autorotating wings: an experimental investigation. Journal of Fluid Mechanics, 50(3), 513-534.

[3] Willmarth, W. W., Hawk, N. E., & Harvey, R. L. (1964). Steady and unsteady motions and wakes of freely falling disks. Physics of Fluids, 7, 197–208.

[4] Field, S. B., Klaus, M., Moore, M. G., & Nori, F. (1997). Chaotic dynamics of falling disks. Nature, 388(6639), 252-254.

[5] Singh, M., Puri, D., & Jakhar, N. (2023). Motion of a sphere in a viscous fluid under controlled acceleration. Physics Education, 59(1), 015012.

[6] Andersen, A., Pesavento, U., & Wang, Z. J. (2005). Unsteady aerodynamics of fluttering and tumbling plates. Journal of Fluid Mechanics, 541, 65-90.