Autor: Adolfo Vázquez Quesada.

Introducción y límite de Roche

Cuando hablamos de anillos planetarios, inmediatamente nos viene a la cabeza la estampa de Saturno. Sin duda, para casi todo el mundo, los anillos hacen de este un planeta más especial. Los de Saturno son los únicos anillos que son observables con telescopios de aficionados desde la Tierra: con un pequeño telescopio refractor de $60\ \text{mm}$ de apertura ya se pueden observar con claridad. No obstante, se han descubierto más anillos en el sistema solar, lo que evidencia que, aunque es impresionante, el caso de Saturno no es un caso único. Como veremos, los anillos ni siquiera son exclusivos de los cuerpos planetarios. Pero, ¿qué es lo que hace que se formen los anillos?. En realidad, no se sabe con certeza cómo se han formado los que hemos observado en el Sistema Solar, pero sí están claros, en el caso de los planetas, algunos de los mecanismos necesarios. Uno de ellos fue propuesto por Édouard Roche en 1848. Este astrónomo hizo un cálculo de la distancia mínima a la que debe estar un satélite de su planeta para que no sea destruido por las fuerzas de marea. A esa distancia mínima se le llama límite de Roche. Se puede hacer una estimación del límite de Roche a partir de principios físicos básicos, así que veamos primero cómo se hace esto.

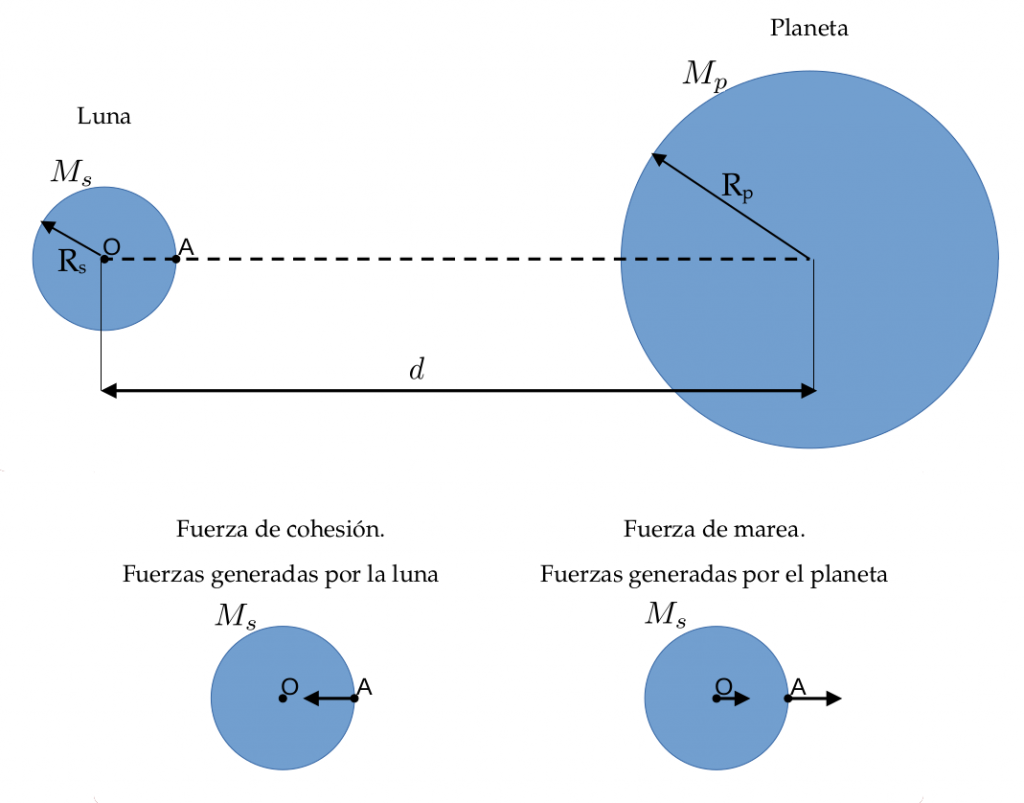
Figura para calcular el límite de Roche. Las fuerzas generadas por la propia luna tienden a hacer que se cohesione. Las fuerzas generadas por el planeta tienden a hacer que se disgregue.

Supongamos que el planeta tiene una masa $M_p$, un radio $R_p$ y una densidad $\rho_p$, y que se encuentra a una distancia $d$ de un satélite de masa $M_s$, de radio $R_s$ y densidad $\rho_s$ (ver la figura de arriba). Para calcular el límite de Roche, tenemos que comparar las fuerzas de cohesión del satélite con las fuerzas de marea que el planeta ejerce sobre este. Por ejemplo, consideremos un cuerpo de masa $m$ en el punto A de la luna (ver la figura de arriba). La luna hará sobre este una fuerza $F_A = -G M_s m / R_s^2$, negativa por ir hacia la izquierda en la figura. Si la masa estuviera en el centro de la luna, punto O, la luna no haría ninguna fuerza sobre esta, pues se encontraría en su centro de masas, y tendría la misma distribución de masa en cualquier dirección que elijamos y en su contraria, anulándose la fuerza gravitatoria. La diferencia entre estas dos fuerzas define una fuerza de cohesión, pues estas hacen que el cuerpo en el punto A sufra una fuerza con dirección y sentido hacia el cuerpo que se encuentra en O, lo que tiende a hacer que el material de la luna se cohesione:
\begin{eqnarray}
F_{\text{cohesión}} = F_A -\ F_O = -G\frac{M_s m}{R_s^2}.
\nonumber
\end{eqnarray}

Por otro lado, el planeta también ejerce una fuerza diferente sobre los cuerpos que están en los puntos A y O de la luna. Si el cuerpo está en A, la fuerza ejercida por el planeta es $F_{A,p} = G M_p m / (d-R_s)^2$, mientras que si el cuerpo está en O, la fuerza ejercida es $F_{O,p} = G M_p m / d^2$. La diferencia entre estas dos fuerzas es lo que se llama fuerza de marea, y esa diferencia tiende a disgregar el cuerpo, pues hace que el cuerpo que está en A tienda a alejarse del cuerpo que está en O, ya que sufre una fuerza mayor el de A que el de O (ver figura de arriba):
\begin{eqnarray}
F_{\text{marea}} = F_{A,p} – F_{O,p} = G\frac{M_p m}{(d-R_s)^2} -\ G\frac{M_p m}{d^2}.
\nonumber
\end{eqnarray}

Lo que va a determinar si el satélite se disgrega o no es la comparación de las fuerzas de cohesión con las fuerzas de marea. Es decir, no comparamos fuerzas, aunque las llamemos así, sino diferencias de fuerzas aplicadas en diferentes puntos. Si la fuerza de marea, que tiende a alejar las masas, es mayor que la fuerza de cohesión, que tiende a acercarlas, entonces el cuerpo tenderá a disgregarse. O dicho de otra manera
\begin{eqnarray}
\text{Si } |F_{\text{cohesión}}| > |F_{\text{marea}}| &\rightarrow& \text{La luna no se disgrega.}
\nonumber\\
\text{Si } |F_{\text{cohesión}}| < |F_{\text{marea}}| &\rightarrow& \text{La luna se disgrega.}
\end{eqnarray}

La condición para calcular el límite de Roche queda entonces, (nótese que en este caso la fuerza de cohesión es negativa, y la de marea positiva)
\begin{eqnarray}
F_{\text{cohesión}} + F_{\text{marea}} = 0 \rightarrow
-G\frac{M_s m}{R_s^2} + G\frac{M_p m}{(d-R_s)^2} -\ G\frac{M_p m}{d^2} = 0
\rightarrow
\frac{M_s}{R_s^2} = \frac{M_p}{d^2}\left(\frac{1}{(1-R_s/d)^2} -\ 1\right).
\nonumber
\end{eqnarray}

Suponiendo que $d \gg R$, podemos hacer una expansión de la fracción, pues para $x$ cercanos a cero $\frac{1}{(1-x)^2}\approx 1 + 2x$, llegando a
\begin{eqnarray}
\frac{M_s}{R_s^2} = 2 \frac{M_p R_s}{d^3},
\nonumber
\end{eqnarray}
de donde se obtiene
\begin{eqnarray}
d = R_s\sqrt[3]{\frac{2 M_p}{M_s}} = R_p\sqrt[3]{\frac{2 \rho_p}{\rho_s}} \approx 1.26 R_p \sqrt[3]{\frac{\rho_p}{\rho_s}}.
\nonumber
\end{eqnarray}
Podéis comprobar que se hubiera obtenido el mismo resultado si, en vez de calcular las fuerzas de cohesión y marea con los puntos A y O, lo hubiéramos hecho con el punto A y su opuesto en la luna.

Como se puede observar en la ecuación, el límite de Roche depende del radio del planeta y de las densidades medias del planeta y del satélite. Nótese también que el cálculo lo hemos hecho para una luna sólida, pero un cálculo para una luna líquida, que no tendría forma esférica sino elipsoidal, da un factor de alrededor de $2.42$ en lugar de $1.26$. Es decir, la luna líquida se disgregaría más lejos que la sólida. Esto se debe a que la luna, por la forma que adquiere, a la misma distancia sufriría una fuerza de marea mayor que en el caso sólido, y, al mismo tiempo, una fuerza de cohesión menor. ¿Pero tiene sentido el cálculo de la luna líquida? Si tenéis en cuenta que las fuerzas de marea generan procesos de fricción, en el interior de las lunas, que pueden fundir el material interno, las lunas no serán en general ni sólidas ni líquidas, y tendrán cierto grado de deformabilidad, especialmente si están tan cerca del planeta, por lo que deberíamos esperar que el factor en casos más realistas fuera algún valor entre $1.26$ y $2.42$.

Un ejemplo de un cuerpo que atraviesa el límite de Roche se dio con el cometa Shoemaker-Levy 9, que fue descubierto en 1993, en órbita elíptica alrededor de Júpiter. Se observó que el cometa estaba ya fragmentado en pequeños trozos y que esto se debió a que el año anterior, el cometa se había acercado a Júpiter a una distancia menor que el límite de Roche. Los fragmentos, finalmente, cayeron en Júpiter aproximadamente un año después, permitiendo ver, por primera vez, una colisión entre cuerpos celestes.

Huella de los impactos de varios fragmentos del cometa Shoemaker-Levy 9 en Júpiter, fotografiados por el telescopio espacial Hubble [1]. Créditos: NASA/Hubble Space Comet Telescope Team.

¿Y por qué los anillos son planos y están en el plano ecuatorial del planeta?

Ya hemos explicado por qué por debajo del límite de Roche no puede haber grandes lunas. Pero, ¿por qué los anillos se encuentran en el plano ecuatorial? La razón de esto está en que el planeta se encuentra más abultado en su zona ecuatorial debido a la rotación del propio planeta, lo que implica que en la latitud ecuatorial del planeta la distribución de masa aumenta, y por tanto, atrae más a un posible anillo que otras latitudes. Dado que el estado mínimo de energía de planeta y anillo se da con el anillo en el plano ecuatorial, por estar más cerca de dicho exceso de masa, los anillos tienden, con el tiempo, a colocarse en el plano ecuatorial.

¿Y por qué son planos? La principal razón de que sean planos se debe a los choques de las partículas entre sí. Supongamos una partícula que se encuentra por debajo del límite de Roche, pero que no orbita en el plano de los anillos. Cada cierto tiempo, cuando pase por el plano de los anillos, chocará con las partículas que los componen, disipándose energía y redistribuyéndo los momentos lineales y angulares de las partículas que chocan, de manera que, de cierta manera, se promedian las órbitas de los cuerpos que colisionan. A la larga, el cuerpo que tenía una órbita inicial inclinada, acabará orbitando en el mismo plano del anillo. En realidad, incluso si no tuviéramos inicialmente un anillo, y hubiera muchas rocas orbitando el planeta, debido a los choques, con el tiempo, todas las rocas acabarían orbitando en anillos.

¿Y por qué son estables los anillos?

En realidad, la estabilidad de los anillos es diferente en cada región, y en algunas de ellas son totalmente inestables. De ahí que veamos divisiones (huecos) en ellos. Existe un teorema del ámbito de los sistemas dinámicos, el Teorema KAM (Kolmogorov-Arnold-Moser), que explica cuándo las órbitas cuasiperiódicas son estables. ¿Y por qué hablamos de órbitas cuasiperiódicas? Porque en la práctica, los objetos del universo no se ven afectados solo por la interacción del cuerpo al que orbitan, sino también por otros cuerpos. Esas otras interacciones podemos considerarlas como perturbaciones sobre la interacción principal, y lógicamente, el movimiento no será, en general, periódico, aunque casi.

En el caso de los anillos, los cuerpos que los forman, además de interactuar con el planeta que orbitan, también están interactuando con los demás cuerpos del anillo, gravitatoriamente y mediante colisiones, así como con las lunas que pueda tener el planeta. El Teorema KAM indica que, si estas perturbaciones son pequeñas, las órbitas cuasiperiódicas serán estables, salvo que haya resonancias en dichas perturbaciones. Por resonancias, nos referimos a que las perturbaciones actúen con un período que forme una fracción sencilla con el período de rotación de la órbita cuasiperiódica de los cuerpos del anillo. Así pues, las regiones de los anillos que estén en resonancia con la órbita de alguna luna serán inestables, y por lo tanto, tenderán a vaciarse. Este fenómeno no es exclusivo de los anillos. Por ejemplo, en el cinturón de asteroides hay ciertas distancias al Sol, denominadas huecos de Kirkwood, en las que la densidad de asteroides prácticamente se anula, debido a la resonancia de las órbitas a esas distancias con la órbita de Júpiter.

Además, si hay alguna pequeña luna dentro del anillo (ha de ser pequeña, pues si no se disgregaría por encontrarse dentro del límite de Roche), esta tenderá a vaciar la región de su órbita, expulsando o atrapando los objetos que haya en ella. Estas son las denominadas lunas pastoras.

Y hasta aquí llega la parte 1 de esta entrada. En la segunda parte, que será publicada próximamente, veremos detalles sobre los anillos que se conocen en el Sistema Solar, incluyendo esos anillos «no tan planetarios» que el título de la entrada promete. !Nos vemos en la parte 2!

Autor: Adolfo Vázquez Quesada.

Adolfo Vázquez Quesada es profesor del Departamento de Física Fundamental de la UNED.

Referencias:

[1] https://nssdc.gsfc.nasa.gov/planetary/sl9/html/hubble_images.html