Autor: Javier Rodríguez Laguna.

Algunos conceptos de física logran escapar de su nicho original y se convierten en metáforas que usa el público en general. Y en ocasiones, el concepto sufre transformaciones en el proceso que dejan perplejas a las personas que inventaron el término.

Algo así ocurrió con el gato de Schrödinger. Ya es estándar leer titulares como «El presidente de Schrödinger», como vemos en la captura. El periodista sugiere así que Donald Trump era presidente y no lo era a la vez. Pero cuando lees el artículo en detalle te das cuenta de que lo que en realidad quiere decir es que no se sabía si Donald Trump llegaría o no a ser presidente. Es decir, se trata de una mera cuestión de probabilidades. Si lanzo una moneda al aire y la tapo con la mano al caer no sé si ha salido cara o cruz. ¿Quiere decir eso que mi moneda es una moneda de Schrödinger?

En un capítulo de The Big Bang Theory, Penny pide a Sheldon su opinión: ¿es buena idea salir con Leonard? Sheldon le cuenta que en 1935 Erwin Schrödinger diseñó un experimento mental en el que un gato era situado en el interior de una caja con un vial de veneno que podría estar abierto o cerrado, dependiendo del momento en el que se desintegrara un cierto núcleo atómico. Consecuentemente, no podrás saber si el gato está vivo o está muerto hasta que abras la caja. Penny piensa que la moraleja de la historia es que debería abrir la caja y probar a salir con Leonard, porque es la única manera de saber si el gato está vivo o está muerto. Sheldon, en realidad, sólo le contaba esa historia para deshacerse de ella, porque el problema no podría interesarle menos.

Siento ponerme pesado, pero… ¡eso no es mecánica cuántica, eso es una mera cuestión de probabilidades, y no era en absoluto lo que Schrödinger tenía en mente!

La teoría de la probabilidad clásica nos habla de nuestra ignorancia. El gato está vivo o muerto, pero nosotros no sabemos en qué estado está, así que representamos nuestro conocimiento sobre el gato en forma de distribución de probabilidad, tal que así.

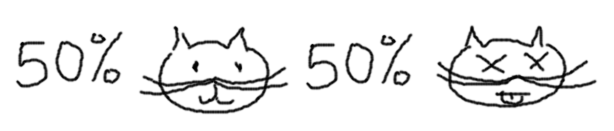
En términos formales decimos que la descripción probabilística tiene carácter epistemológico: describe lo que sé y lo que no sé sobre el gato. En cambio, la mecánica cuántica realiza una descripción ontológica, es decir, te describe el estado real del gato, no lo que yo sé sobre él. En nuestro caso, dado que el evento de la desintegración del núcleo es cuántico, la manera «correcta» de describir al gato es a través de una superposición de estados:

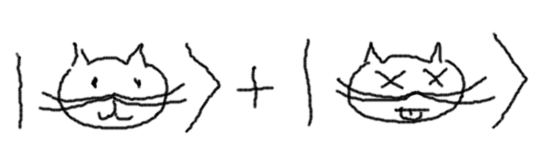
He usado la notación más usual en mecánica cuántica, llamada de Dirac, en la que cada estado se representa mediante un ket: |gato-vivo> y |gato-muerto> serían dos estados diferentes que puedo superponer. No sólo me permiten sumarlos, sino también restarlos, o multiplicarlos por un número arbitrario. Pero eso no es importante ahora, así que regresemos a nuestra superposición. La clave es que este estado, superposición de gato-vivo y gato-muerto es un nuevo estado gatúnico:

Y este nuevo estado tiene propiedades diferentes. Si abrimos la caja y medimos el observable VIDA aplicado al gato, la mecánica cuántica nos dice que el resultado será SÍ o NO con un 50% de probabilidades, y que el estado colapsará a uno de los dos estados en los que la VIDA está bien definida: |gato-vivo> o |gato-muerto>. Pero la mecánica cuántica también nos dice que existe otro observable, que podemos llamar LOCURA, que aplicado sobre |gato-vivo>+|gato-muerto> nos dirá SÍ, y dejará al estado igual.

¿Suena absurdo? Claro, y eso es lo que Schrödinger pretendía: sacar a la luz la componente antiintuitiva de la idea. Pero absurda sólo lo es cuando la aplicamos a gatos. Normal, podéis pensar: los gatos no se dejan manipular así como así, chillan, maúllan y arañan para evitarlo. Pero es que si lo hacemos con fotones o con electrones, es realmente lo que sucede.

Imaginad un electrón, y centrémonos en un sólo aspecto: su estado de espín. El espín se puede imaginar como un momento angular intrínseco… sólo que no es eso.

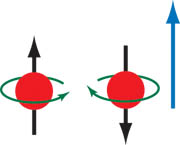
Decimos que el electrón tiene espín 1/2, y eso implica que todo estado de espín puede describirse como superposición de dos estados, que podemos llamar «espín-hacia-arriba» o «espín-hacia-abajo». En la jerga cuántica, escribimos $|\uparrow\rangle$ y $|\downarrow\rangle$. Perfecto. Ahora escribamos una superposición de ambos, por ejemplo

$$|\uparrow\rangle + |\downarrow\rangle$$

Ahora consideremos el observable «Componente Z del espín», que podemos llamar $S_Z$. Si medimos $S_Z$ obtendremos el resultado «hacia arriba» con probabilidad 1/2 o «hacia abajo» con probabilidad 1/2. ¿Quiere eso decir que tenemos un estado probabilístico, sin más? No. La razón es que existen otros observables que nos dan una respuesta segura. Por ejemplo, si medimos $S_X$, es decir, la «Componente X del espín«, podemos obtener dos respuestas, «espín-hacia-la-izquierda» o «espín-hacia-la-derecha». Y, adivinad qué ocurre: cuando mido $S_X$ sobre el estado anterior, obtengo «espín-hacia-la-derecha» el 100% de las veces.

De ahí concluyo que mi estado $|\uparrow\rangle + |\downarrow\rangle$ no es una mera mezcla estadística de dos estados, sino que es algo más. Es un espín que apunta hacia la derecha. Cuando le preguntamos si apunta hacia arriba o hacia abajo, pues no tiene ni idea, y se lo inventa.

Entonces, ¿qué pasaría con un espín que apunta hacia la izquierda? Seguro que ya se le ha ocurrido a alguno/a. Tenemos:

$$|\uparrow\rangle + |\downarrow\rangle = |\text{Espín a la derecha}\rangle$$

$$|\uparrow\rangle\, -\, |\downarrow\rangle = |\text{Espín a la izquierda}\rangle$$

Y con eso hemos cubierto dos direcciones espaciales. ¿Qué sucede en la tercera? Es decir, ¿cómo son los estados de espín 1/2 que «apuntan» en el eje Y? Bueno, eso os lo dejamos como ejercicio.

En mecánica cuántica distinguimos entre estados puros (que son los estados «reales», máximamente determinados, y sus superposiciones) y estados mezcla, que son meras combinaciones estadísticas de estados puros. Por ejemplo, supongamos que tiro una moneda y preparo un espín como $|\uparrow\rangle$ o $|\downarrow\rangle$ dependiendo de lo que salga. Eso es un estado mezcla. Pero si preparo un espín como $|\uparrow\rangle + |\downarrow\rangle$ entonces tengo un estado puro, que apunta hacia la derecha. Lo que pasa es que si me empeño en medir $S_Z$, se comporta igual que un estado mezcla.

¿Y los gatos? Pues ahí está la pregunta relevante. ¿Se puede crear un estado puro que sea superposición de gato-vivo y gato-muerto? Nadie lo ha conseguido hasta ahora. Se han creado estados superposición de electrones, fotones, átomos, moléculas… El récord, hasta donde sé, es un enorme cristal de zafiro de 16 microgramos. Con gatos nadie lo ha logrado, ni siquiera con los pequeñitos. Pero nada parece impedirlo a nivel fundamental.

¿Y entonces, por qué no podemos construir superposiciones cuánticas de estados gatúnicos? Por más que lo intento, al final los gatos sólo me aparecen borrosos cuando tengo las gafas empañadas… Pues la respuesta no está del todo clara. Las superposiciones cuánticas suelen ser frágiles, y aún nos quedan muchas preguntas al respecto. En general, cuanto más interactúa un objeto con su entorno más corto será su tiempo de coherencia, es decir, el tiempo que es capaz de mantenerse en superposición. Así, cuanto más grande es el objeto, o cuanto mayor es la temperatura, menor será su tiempo de coherencia. Sabemos mucho más sobre el problema que en tiempos de Schrödinger, hace 90 años, pero el puzzle está lejos de estar completo.

Autor: Javier Rodríguez Laguna.

Javier Rodríguez Laguna es profesor del Departamento de Física Fundamental de la UNED.