Autor: Manuel Pancorbo Castro.
Introducción
Cuando se introduce la Relatividad Especial en el Bachillerato, se explica que la velocidad de la luz es un límite intraspasable, que ello conlleva unas transformaciones entre sistemas que son un poco más complicadas que las de Galileo y que eso afecta al concepto de simultaneidad. Se habla de la «dilatación del tiempo» de los observadores en el sistema que se desplaza, y de la «contracción de las longitudes» medidas desde el sistema en reposo. Incluso a veces se dan fórmulas; por ejemplo, la longitud que mide el observador en reposo de una vara que mide $L_\circ$, y que se desplaza a velocidad $v$ en sentido longitudinal, es: \begin{eqnarray}
L = L_\circ \sqrt{1-\frac{v^2}{c^2}}.
%%\tag{1}
\end{eqnarray}
Llegados a este punto, ahora se menciona que la masa que mide el observador en el sistema de laboratorio aumenta con la velocidad y se introducen los conceptos de «masa relativista», $m_{rel}$ y «masa en reposo», $m_\circ$, de forma que:
\begin{equation} m_{rel} = \gamma \,m_\circ,\ \ \ \ \ (1)\end{equation} donde se introduce el factor de Lorentz, $\gamma = 1/\sqrt{1-v^2/c^2}$.
Veamos ahora si esto está justificado.
Momento lineal
En Relatividad Especial, el momento de una partícula medido por el observador en el sistema de laboratorio tiene la expresión:
\begin{equation}
p = \gamma\,m_\circ v, \ \ \ \ \ (2)
\end{equation} que muy bien podría reinterpretarse como: $p = (\gamma\,m_\circ) v = m_{rel}\, v$, a partir de la expresión (1) y que no es más que la fórmula del momento lineal clásico, $p = m_\circ v$, sin más que sustituir $m_\circ$ por $m_{rel}$. Por tanto, parecería apropiado introducir el concepto de masa relativista como reflejo de que, bajo la perspectiva de la visión clásica del momento lineal, que es proporcional a la velocidad, la inercia de la partícula va aumentando conforme nos acercamos al límite $v \rightarrow c$.
Pero veamos qué ocurre con la energía cinética.
Energía cinética
La energía cinética clásica tiene la expresión:
\begin{equation}
E_k = \frac{1}{2} m_\circ v^2,\ \ \ \ \ (3)
\end{equation} y tendríamos que ver si la energía cinética relativista se puede expresar sustituyendo la masa en reposo por la relativista en la expresión (3):
\begin{equation}
E_k = \frac{1}{2} m_{rel} v^2 = \frac{1}{2} \gamma\, m_\circ v^2 ,\ \ \ \ \ (4)
\end{equation} lo que daría el espaldarazo definitivo al concepto de masa relativista.
Energía relativista
La energía de una partícula relativista surge a partir de la expresión:
\begin{equation}
E^2 = m_\circ^2 c^4 + p^2 c^2.\ \ \ \ \ (5)
\end{equation} Sustituyendo la ecuación (2): \begin{equation}
E^2 = m_\circ^2 c^4 + \frac{ m_\circ^2 v^2 c^2}{1- v^2/c^2}
= \frac{m_\circ^2 c^4}{1- v^2/c^2},
\end{equation} de donde: \begin{equation}
E = \frac{m_\circ c^2}{\sqrt{1- v^2/c^2}}.
\end{equation}
Antes de seguir observemos la característica sorprendente de la Relatividad Especial de que, incluso en reposo, la partícula tiene una energía $E = m_\circ c^2$, que es lo que en la cultura popular se conoce como «ecuación de Einstein».
Obsérvese que, en todo este análisis, subrepticiamente hemos escamoteado el concepto de «energía cinética» y hemos hablado genéricamente de «energía». Por tanto, para hablar propiamente de energía cinética tenemos que sustraer la energía en reposo de la energía total:
\begin{equation}
E_k = E\ -\ m_\circ c^2 = m_\circ c^2 (\gamma\ -\ 1), \ \ \ \ \ (6)
\end{equation} donde hemos recuperado la definición de $\gamma$.
A estas alturas parece claro que no podemos obtener la energía cinética correcta, ecuación (6), simplemente de la ecuación (4).
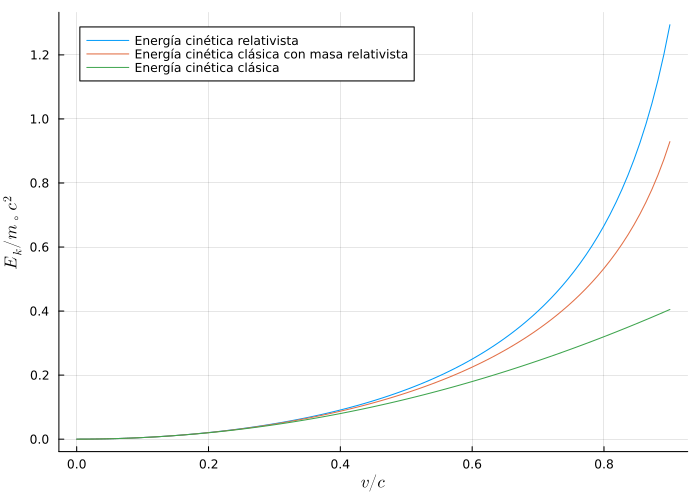
Figura 1: Comparación de energías cinéticas. En el Anexo, al final de la página, se incluye el código del lenguaje de programación Julia utilizado para generar esta gráfica.
Por si acaso la comparación entre ambas ecuaciones no fuera suficiente, y sospechamos que por algún arcano truco algrebraico ambas podrían ser coincidentes, entonces no tenemos más que mirar en la Figura 1, donde representamos cómo varian con la velocidad la energía cinética verdadera, Ecuación (6), y la presupuesta a partir de la masa relativista, Ecuación (4); por completitud se añade también la energía cinética clásica.
Conclusión
Definitivamente, el concepto de masa relativista no se sostiene y debería ser descartado del relato que se hace de la Relatividad Especial en el Bachillerato y en el contexto de la divulgación científica.
Esto es más evidente porque la expresión (5) surge a partir de la contracción del cuadrivector energía-momento. En Relatividad, las magnitudes vectoriales se expresan como un vector de cuatro dimensiones —una de ellas sería la componente en la dimensión temporal— y su contracción, que es una operación parecida a la norma de un vector tradicional, da como resultado siempre un invariante, esto es, una magnitud escalar que es siempre la misma en cualquier sistema de referencia. En el caso del cuadrivector energía-momento, su contracción no es más que la masa: \begin{equation}
\frac{E^2}{c^2}\ -\ p^2 = m_\circ^2 c^2,
\end{equation} expresión a partir de la cual obtenemos la ecuación (5). Por tanto, la masa es única y no cabe la distinción entre «masa en reposo» y «masa relativista».
Epílogo
Es posible que el título de este artículo haya podido causar la impresión de que el tema del mismo es la hipótesis de la igualdad de la masa inercial y la gravitatoria, que es uno de los postulados de la Relatividad General.
No es el caso, obviamente. Al respecto solo puedo añadir que, si bien no deja de ser una hipótesis, no hay ningún experimento, hoy por hoy, que la haya cuestionado.
Autor: Manuel Pancorbo Castro.
Manuel Pancorbo Castro es profesor del Departamento de Física Interdisciplinar de la UNED.
Anexo: Código del lenguaje de programación Julia para generar la figura 1.
## Código en lenguaje 'julia' para hacer la gráfica
## de las energías
using Plots
using LaTeXStrings
v = range(0, 0.9, length=100) # Velocidades
E1 = 1 ./sqrt.(1.0 .- v.^2) .- 1.0 # Energía relativista
E2 = 0.5 * v.^2 ./ sqrt.(1.0 .- v.^2) # Energía clásica con masa relativista
E3 = 0.5 *v.^2 # Energía clásica
plot(v, E1,
label="Energía cinética relativista"
)
plot!(v, E2,
label="Energía cinética clásica con masa relativista"
)
plot!(v, E3,
label="Energía cinética clásica"
)
xlabel!(L"v/c")
ylabel!(L"E_k/m_\circ c^2")