Autor: Adolfo Vázquez Quesada.

En el rico ecosistema numérico, una de las presas más preciadas son los mínimos. Los beneficios de la depredación de mínimos son grandes, pues permiten encontrar estados de equilibrio estables, o ajustar datos a funciones mediante el método de mínimos cuadrados, entre otros muchos provechos que pueden sacar de ello sus depredadores. Para cazar a estas fascinantes criaturas, estrategias como agazaparse en la oscuridad y esperar a que aparezcan para emboscarlas no darán frutos, pues los mínimos permanecen quietos, siempre en el mismo lugar, fascinados por la disposición de los gradientes que ven a su alrededor divergiendo del punto en el que se encuentran: el mínimo de la función.

Una de las estrategias más productivas que usan los depredadores de mínimos, es la de ir descendiendo por los gradientes, lo que en inglés se llama gradient descent, hasta conseguir atraparlos. Recordemos que los gradientes indican la dirección en la que la función crece más rápido, por lo que recorrerlos en sentido contrario ayuda a encontrar a los mínimos. No obstante, muchos mínimos se esconden entre gradientes tan grandes que es difícil seguirlos hasta el lugar en el que está el mínimo sin pasarse. Otros mínimos se colocan en lugares en los que obtener el valor de la función en un punto es ya muy difícil, como cuando los datos de esta vienen de simulaciones o de experimentos, lo que hace que calcular el gradiente sea aún más complicado. A veces también se esconden en espacios de tantas dimensiones que resulta complicado saber hacia dónde se dirige el gradiente. Pero existe un fascinante depredador que puede tener éxito en donde otros fallan y que es el protagonista de nuestro documental: la ameba.

La ameba a la que nos referimos es un poco diferente de la que encontramos en el mundo natural. Los matemáticos la denominan símplex, y puede medrar en espacios con cualquier número de dimensiones. Su forma es la de un politopo (un poliedro de caras planas) y tiene un vértice más que dimensiones tenga el espacio en el que vive. Por ejemplo, si vive en un espacio de dos dimensiones, tiene tres vértices y forma de triángulo. Si vive, en un espacio tridimensional, tiene cuatro vértices y forma de tetraedro, y así sucesivamente. En general, si la ameba vive en un espacio de $N$ dimensiones, tiene $N+1$ vértices.

Esta ameba es implacable cuando caza a un mínimo y basa su táctica en ir reptando por el espacio acercándose a él paso a paso. El éxito de la caza dependerá de lo bien que se mueva la ameba. Estos depredadores son despiadados y siempre hacen sus movimientos de la misma manera, acercándose cada vez más al indefenso mínimo. Las amebas son muy sistemáticas y siguen una serie de pasos por orden de manera estricta. Acampañadnos en este ejemplo típico de caza de uno de estos deprededadores:

1. El arma principal de la ameba está en su capacidad de evaluar con precisión la función $f$ en varios puntos clave. Sus finos sentidos le permiten calcular, por ejemplo, la función en sus vértices. De hecho, en cada paso de su caza, es lo primero que hace, para luego ordenarlos. En la mente de la ameba, su vértice $1$ es el vértice que mejor valor tiene, es decir, con un valor de $f$ más bajo, mientras que el peor vértice es el $N+1$. De esta manera, se cumplirá que $f(\vec{\boldsymbol{r}}_1)\le f(\vec{\boldsymbol{r}}_2)\le\ldots \le f(\vec{\boldsymbol{r}}_{N+1})$. La ameba sabe que su vértice $\vec{\boldsymbol{r}}_1$ está en una buena posición, pero no está tan contenta con la posición que tiene su vértice $\vec{\boldsymbol{r}}_{N+1}$, por lo que querrá cambiar la posición de este vértice lo antes posible.
2. En un segundo paso, la ameba prepara su asalto, antes de moverse, evaluando la función en el centroide $\vec{\boldsymbol{r}}_0$ de todos los vértices salvo el $N+1$. La ameba quiere que, de alguna forma, el vértice en $\vec{\boldsymbol{r}}_{N+1}$ se acerque a los demás, y por lo tanto, a $\vec{\boldsymbol{r}}_0$.
3. La ameba quiere quitar su vértice de la posición $\vec{\boldsymbol{r}}_{N+1}$ y piensa que debería moverlo más hacia el resto de vértices, que tienen mejores posiciones. Se plantea entonces hacer una reflexión de dicho vértice respecto a $\vec{\boldsymbol{r}}_0$. Para ello, tantea la posición $\vec{\boldsymbol{r}}_r = \vec{\boldsymbol{r}}_0 + \alpha\left(\vec{\boldsymbol{r}}_0-\vec{\boldsymbol{r}}_{N+1}\right)$. El valor $\alpha=1$ ha sido observado en muchas amebas, de manera que la reflexión sea simétrica respecto de $\vec{\boldsymbol{r}}_0$. Si nuestra protagonista ve que $f(\vec{\boldsymbol{r}}_0)$ es mejor que el segundo peor vértice, el $N$, pero peor que el vértice $1$, entonces la ameba directamente coloca su vértice ahí, sustituyendo la posición $\vec{\boldsymbol{r}}_{N+1}$ por la $\vec{\boldsymbol{r}}_0$. Si la ameba hace esto, empezará un nuevo movimiento volviendo al paso 1. Sin embargo, si la condición anterior no se cumpliera, entonces la ameba no haría nada todavía y pasaría al paso 4.

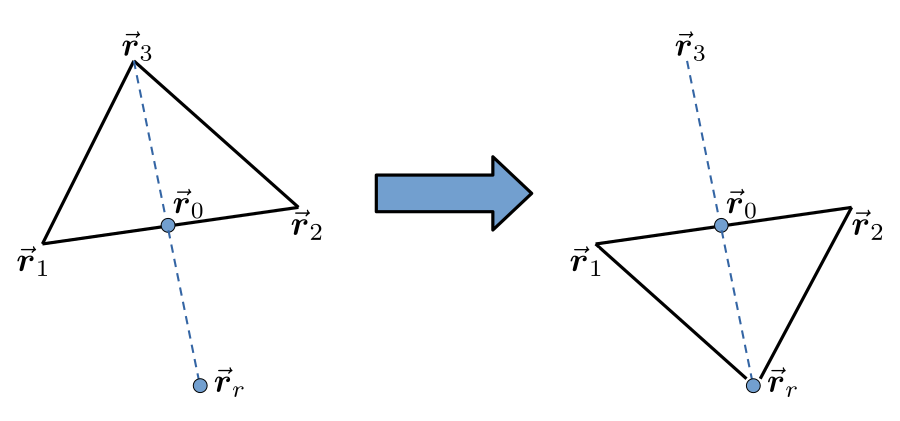
En esta imagen observamos a una ameba en plena caza. La ameba, que medra en el espacio $(x,y)$, es decir $N=2$, ha hecho una reflexión.

4. Aquí se pueden dar dos posibilidades:

• La primera posibilidad es que la ameba, en el paso anterior, haya visto que el valor de $f$ en $\vec{\boldsymbol{r}}_r$ es mejor que en la mejor posición que tenía, es decir, que en $\vec{\boldsymbol{r}}_1$. En este caso se volverá más ambiciosa e intentará ver si más allá de $\vec{\boldsymbol{r}}_r$ los valores de $f$ pueden ser incluso mejores. Si fuera así, la ameba querría hacer una expansión hacia dicha región. Para comprobar esto, tantea entonces la posición $\vec{\boldsymbol{r}}_e = \vec{\boldsymbol{r}}_0 + \gamma\left(\vec{\boldsymbol{r}}_r-\vec{\boldsymbol{r}}_0\right)$, en donde $\gamma > 1$. Un valor típico observado por los estudiosos de las amebas es $\gamma = 2$. Si la ameba ve que $\vec{\boldsymbol{r}}_e$ es incluso mejor que $\vec{\boldsymbol{r}}_r$, moverá sin dudar su vértice desde $\vec{\boldsymbol{r}}_{N+1}$ hasta $\vec{\boldsymbol{r}}_e$. Sin embargo, si la ameba viera que $\vec{\boldsymbol{r}}_e$ no es mejor que $\vec{\boldsymbol{r}}_r$, se conformará con cambiar su vértice de la posición $\vec{\boldsymbol{r}}_{N+1}$ a $\vec{\boldsymbol{r}}_r$. Tras hacer cualquiera de estas dos cosas, la ameba comenzará de nuevo volviendo al paso 1.
• La otra posibilidad es que $\vec{\boldsymbol{r}}_r$ no sea mejor que $\vec{\boldsymbol{r}}_1$. En este caso, la ameba se armará de paciencia y pasará al paso 5.

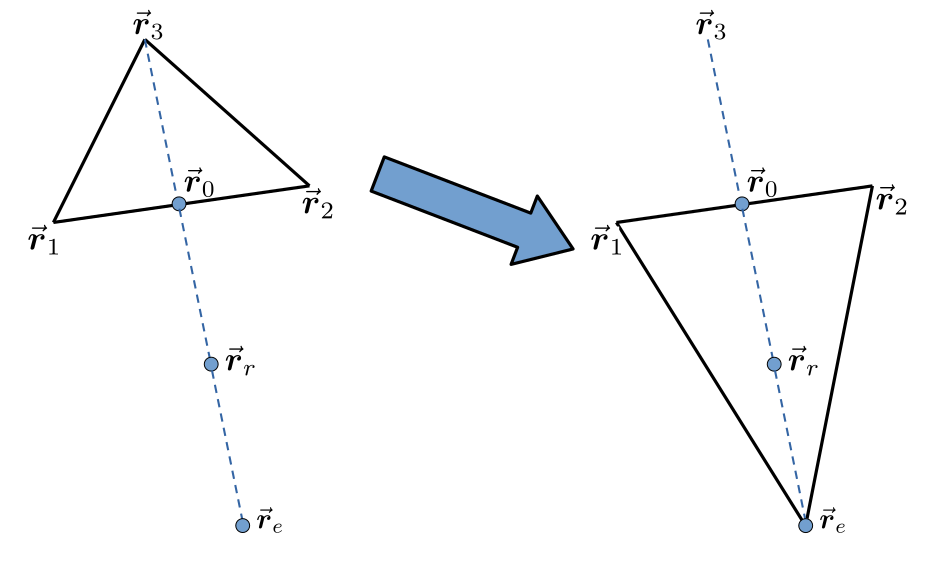
La ameba, en su búsqueda del mínimo, hace una expansión.

5. Si la ameba llega a este paso, significa que la posición $\vec{\boldsymbol{r}}_r$ es peor que la segunda peor posición, $\vec{\boldsymbol{r}}_{N}$. La ameba creerá entonces que el mínimo está cerca de $\vec{\boldsymbol{r}}_0$. Se plantea entonces hacer una contracción. De nuevo hay dos posibilidades aquí:

• En el caso de que $\vec{\boldsymbol{r}}_r$ sea mejor que $\vec{\boldsymbol{r}}_{N+1}$, es decir, $f(\vec{\boldsymbol{r}}_r) < f(\vec{\boldsymbol{r}}_{N+1})$, entonces tanteará el punto $\vec{\boldsymbol{r}}_{c1} = \vec{\boldsymbol{r}}_0 + \rho\left(\vec{\boldsymbol{r}}_r-\vec{\boldsymbol{r}}_0\right)$, con $0<\rho\le 0.5$. Este punto se encuentra cerca de $\vec{\boldsymbol{r}}_0$, pero en el lado contrario a $\vec{\boldsymbol{r}}_{N+1}$. Si la función en $\vec{\boldsymbol{r}}_{c1}$ es menor que en $\vec{\boldsymbol{r}}_r$, entonces la ameba moverá su vértice desde $\vec{\boldsymbol{r}}_{N+1}$ hasta $\vec{\boldsymbol{r}}_{c1}$. Tras esto, comenzará su próximo movimiento, volviendo al paso 1. Pero en caso de que $f\left(\vec{\boldsymbol{r}}_{c1}\right)$ no sea menor que $f(\vec{\boldsymbol{r}}_{N+1})$, entonces la ameba relamiéndose, ejecutará al paso 6.
• Si $\vec{\boldsymbol{r}}_r$ fuera peor que $\vec{\boldsymbol{r}}_{N+1}$, la ameba probará con el punto $\vec{\boldsymbol{r}}_{c2} = \vec{\boldsymbol{r}}_0 + \rho\left(\vec{\boldsymbol{r}}_{N+1}-\vec{\boldsymbol{r}}_0\right)$, con $0<\rho\le 0.5$. El punto $\vec{\boldsymbol{r}}_{c2}$ es un punto cercano a $\vec{\boldsymbol{r}}_0$ y en el mismo lado que $\vec{\boldsymbol{r}}_{N+1}$. Si la función en $\vec{\boldsymbol{r}}_{c2}$ es menor que en $\vec{\boldsymbol{r}}_{N+1}$, entonces la ameba moverá su vértice desde $\vec{\boldsymbol{r}}_{N+1}$ hasta $\vec{\boldsymbol{r}}_{c2}$ y comenzará un nuevo movimiento, volviendo al paso 1. Si no fuera así, la ameba, tenaz, ejecutará el paso 6.

Los estudiosos de las amebas han reportado valores típicos de $\rho$ de $0.5$.

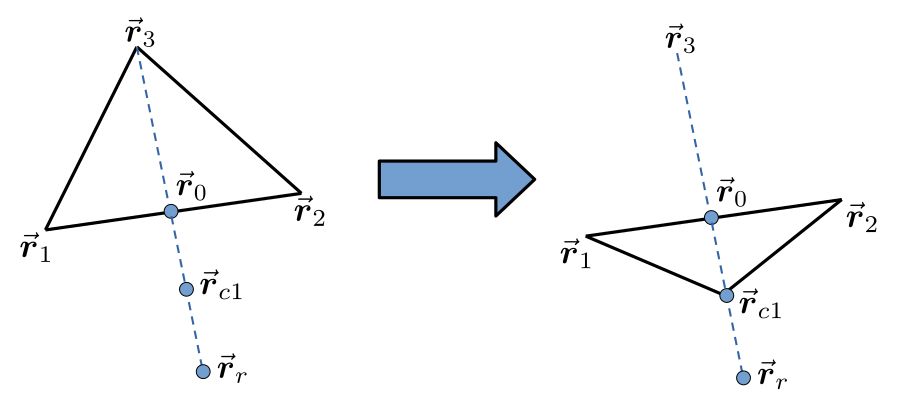
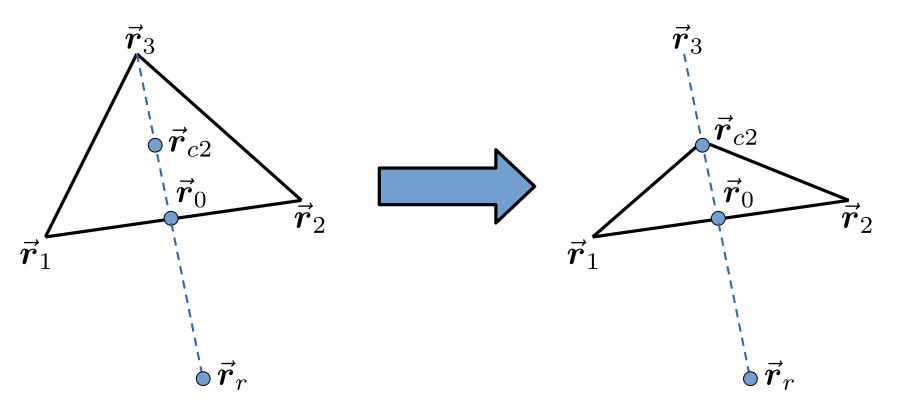
Los dos tipos de contracción observados en las amebas.

6. Si la ameba ha llegado a este paso, sospechará que el mínimo se encuentra en alguna posición cerca de su mejor vértice, $\vec{\boldsymbol{r}}_1$. Decide entonces encogerse hacia su vértice prederido, $\vec{\boldsymbol{r}}_1$, cambiando todos los demás de posición. Así pues, todos los vértices $i$, salvo el $1$, se trasladan a las siguientes posiciones: $\vec{\boldsymbol{r}}_i = \vec{\boldsymbol{r}}_1 + \sigma\left(\vec{\boldsymbol{r}}_i-\vec{\boldsymbol{r}}_1\right)$. Los más avezados observadores dicen haber visto en muchas amebas un valor de $\sigma$ de $0.5$. Tras encogerse, la ameba inicia confiada su siguiente movimiento, volviendo al paso 1.

En la búsqueda de su presa la ameba hace un escalofriante y preciso movimiento, encogiéndose.

En las siguientes imágenes se ha captado la secuencia de caza de una ameba. En la impactante escena, se puede observar cómo el incauto mínimo de la función $f(x)=\left(x^2 – 2y\right)^2 + (x-y)^2 + x + 5$, que se ve como un punto rojo, enfrenta, sin ser consciente, sus últimos momentos. En el aparentemente tranquilo paisaje de los gradientes de la función, que se ven como flechas azules, aparece sin previo aviso la ameba por la esquina superior derecha. El ataque de la ameba es rápido y devastador para el mínimo, que solo se da cuenta de lo que sucede ya en el último instante.

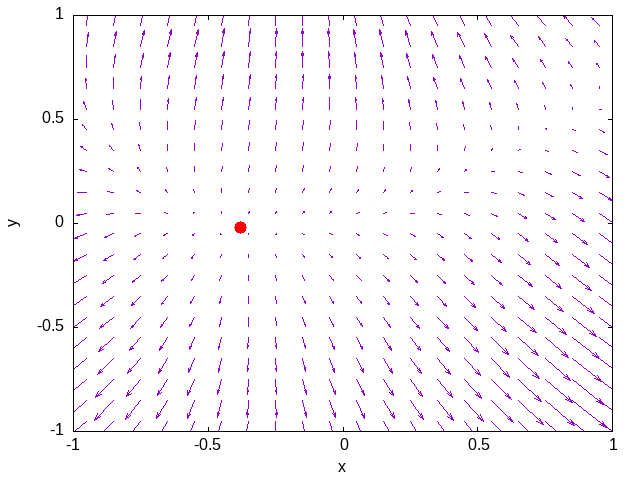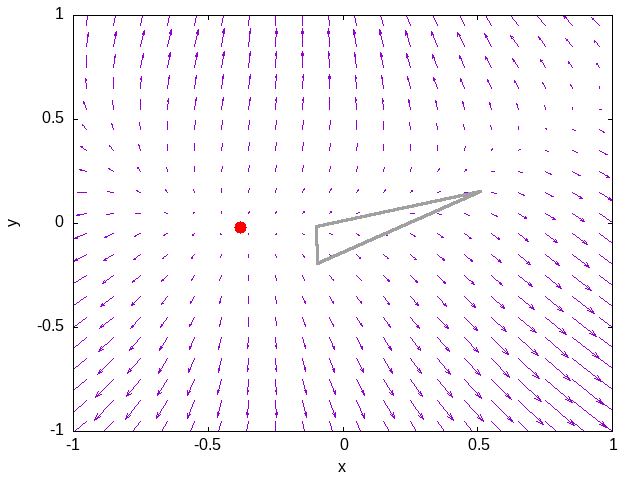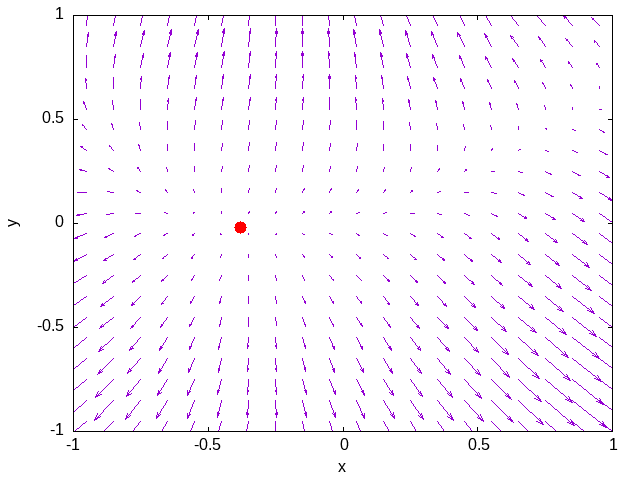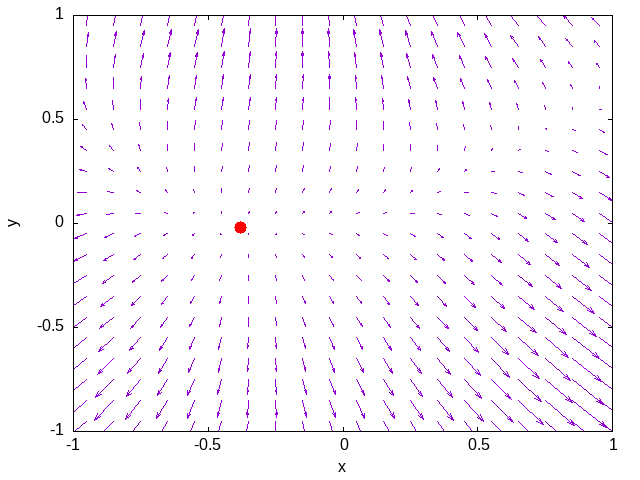
PD: Por si tenéis interés en saber más detalles sobre este método para buscar mínimos, aunque conocido también como el método de la ameba, es más conocido como método de Nelder-Mead.

Autor: Adolfo Vázquez Quesada.

Adolfo Vázquez Quesada es profesor del Departamento de Física Fundamental de la UNED.

Referencias:

• Nelder, J. A., & Mead, R. (1965). A simplex method for function minimization. The computer journal, 7(4), 308-313.
• http://var.scholarpedia.org/article/Nelder-Mead_algorithm