Autor: Adolfo Vázquez Quesada.

La cinemática es la rama de la física que se dedica a estudiar el movimiento de los objetos. Normalmente es el primer capítulo en prácticamente todos los cursos de física general, pues lo interesante de los procesos físicos es casi siempre el estudio de algo cuyo movimiento cambia, ya sea por fuerzas gravitatorias, electromagnéticas o de otro tipo. El tema de la cinemática suele ser siempre bastante anodino: no creo que haya mucha gente que se meta a estudiar física con un interés profundo en la cinemática. Digamos que es un tema necesario para poder dedicarse a otras tareas más satisfactorias en las que la cinemática es necesaria porque las cosas se mueven. Esto nos lleva a una aparente contradicción: la cinemática es aburrida, pero las cosas son más interesantes si su movimiento cambia. Entonces, ¿cómo puede ser aburrida la cinemática si con ella estudiamos cosas interesantes?

Quizás el problema de la ‘cinemática aburrida’ se encuentre en el enfoque que se le suele dar: es una materia que se introduce en cursos preuniversitarios y que casi siempre se enseña con un enfoque más parecido al de un zoólogo del siglo XIX que al de un físico. Entre las criaturas de nuestro ‘zoológico cinemático’ destacan las siguientes:
– Movimiento rectilíneo uniforme (MRU)
– Movimiento rectilíneo uniformemente acelerado (MRUA)
– Movimiento circular uniforme (MCU)
– Movimiento circular uniforme (MCUA)
cada una con sus particularidades que la definen, y en cada caso con unas siglas que les otorgan un carácter más elevado y que podrían ser equivalentes a los nombres científicos latinos de las especies que tan bien hacían quedar a los biólogos decimonónicos. No obstante, es fácil que este enfoque nos lleve a creer que toda la ‘fauna cinemática’ se puede representar por estas cuatro especies, y puede que alguna más, cuando en realidad, tiene muchas más que cuatro: infinitas, de hecho. Sólo hace falta que nos fijemos bien en nuestro propio movimiento desde la panadería hasta casa para darnos cuenta de ello. Pero la pátina técnico-científica de semejantes siglas puede hacer dudar a cualquiera de lo que sus propios sentidos observan.

Un enfoque que, al menos desde mi punto de vista, parece mucho más interesante, es el de invocar a las dos ecuaciones que gobiernan a todas estas ‘especies cinemáticas’, algo que difícilmente podrán hacer los biólogos con las especies de verdad, pero que resulta bastante sencillo para un físico. Las dos ecuaciones son las definiciones de velocidad y aceleración instantáneas, $\vec{\boldsymbol{v}}$ y $\vec{\boldsymbol{a}}$ respectivamente, dadas por \begin{eqnarray}
\vec{\boldsymbol{v}} &=& \frac{d\vec{\boldsymbol{r}}}{dt}, \ \ \ \ \ (1)
\label{def_v}\\
\vec{\boldsymbol{a}} &=& \frac{d\vec{\boldsymbol{v}}}{dt}, \ \ \ \ \ (2)
\label{def_a}
\end{eqnarray} siendo $\vec{\boldsymbol{r}}$ la posición del móvil y $t$ el tiempo. Todos los movimientos que podamos imaginar se regirán por estas ecuaciones, pues son definiciones, incluidos los cuatro individuos estrella de los primeros temas de los cursos de física general, indicados arriba. Como vemos, estas definiciones utilizan derivadas, y para poder aplicarlas apropiadamente a cualquier movimiento también habrá que hacer integrales, por lo que es un enfoque que, en principio, sólo se podrá tomar cuando ya dominemos el uso de la derivada y la integral. Pero que eso no asuste a nadie: es un dominio a muy bajo nivel el que se requiere: si sabemos hacer las derivadas e integrales más básicas ya estaremos preparados para enfrentarnos a la tarea que tenemos entre manos: mostrar que las ecuaciones de nuestras cuatro ‘criaturas cinemáticas’ se pueden encontrar partiendo sólo de estas dos ecuaciones. Antes de empezar, me gustaría enfatizar que no estoy abogando porque deduzcáis siempre las ecuaciones cada vez que las necesitéis. De cara a un examen, por ejemplo, conviene aprender algunas ecuaciones específicas de cada movimiento (solo algunas), o correréis el riesgo de que la nota se empobrezca por falta de tiempo. Pero es muy aconsejable hacer este ejercicio en algún momento, pues da mucha tranquilidad mental y aplomo en el cálculo cuando uno sabe de dónde viene la ecuación que está utilizando. Sin más dilación, vayamos dominando a cada una de nuestras criaturas.

Movimiento rectilíneo uniforme
Este movimiento se define con una única característica: es de velocidad constante. Notad que no hace falta decir que es rectilíneo, pues la velocidad es un vector, y si es un vector constante, lo será tanto en módulo como en dirección y sentido. Por lo tanto, que la velocidad sea un vector constante ya implica que el movimiento sea rectilíneo. Utilizando la definición de velocidad, ecuación (1), podemos operar como se muestra a continuación \begin{eqnarray}
\vec{\boldsymbol{v}} = \frac{d\vec{\boldsymbol{r}}}{dt}
\ \rightarrow\ d\vec{\boldsymbol{r}} = \vec{\boldsymbol{v}}dt
\ \rightarrow\ \int_{\vec{\boldsymbol{r}}_0}^{\vec{\boldsymbol{r}}}d\vec{\boldsymbol{r}} = \int_0^t\vec{\boldsymbol{v}}dt
\ \rightarrow\ \vec{\boldsymbol{r}} = \vec{\boldsymbol{r}}_0 + \vec{\boldsymbol{v}}t. \ \ \ \ \ (3)
\label{pos_MRU}
\end{eqnarray} La ecuación obtenida es la fórmula de la posición del movimiento rectilíneo uniforme.Si te genera dudas hacer integrales de vectores, puedes plantear y resolver la ecuación para cada componente del vector. Por ejemplo, en el eje x habría que resolver $v_x = dx/dt$. Si aplicamos la definición de la aceleración, ecuación (2), dado que $\vec{\boldsymbol{v}}$ no varía con el tiempo, se obtendrá que la aceleración es nula: \begin{eqnarray}
\vec{\boldsymbol{a}} = \frac{d\vec{\boldsymbol{v}}}{dt} = \vec{\boldsymbol{0}}.
\end{eqnarray}

Movimiento rectilíneo uniformemente acelerado
Este se define como un movimiento de aceleración constante y es rectilíneo. En este caso, sí que hace falta especificar que es rectilíneo, porque una aceleración constante no lo asegura. Por ejemplo, si la velocidad inicial de un objeto no es paralela a la aceleración que tiene, esta cambiará la dirección de la velocidad y, por lo tanto, el movimiento no será rectilíneo. Así pues, la definición del movimiento implica que el vector $\vec{\boldsymbol{a}}$ no cambie con el tiempo y que la velocidad inicial $\vec{\boldsymbol{v}}_0$ tenga la misma dirección que $\vec{\boldsymbol{a}}$. Utilizando la definición de aceleración, ecuación (2), podemos operar como se muestra a continuación \begin{eqnarray}
\vec{\boldsymbol{v}} = \frac{d\vec{\boldsymbol{r}}}{dt} \ \rightarrow \
d\vec{\boldsymbol{r}} = \vec{\boldsymbol{v}} dt \ \rightarrow \
\int_{\vec{\boldsymbol{r}}_0}^{\vec{\boldsymbol{r}}}d\vec{\boldsymbol{r}} = \int_0^t\vec{\boldsymbol{v}} dt
\ \rightarrow \
\vec{\boldsymbol{r}} \ – \ \vec{\boldsymbol{r}}_0 = \int_0^t\left(\vec{\boldsymbol{v}}_0 + \vec{\boldsymbol{a}}t\right) dt
\ \rightarrow \
\vec{\boldsymbol{r}} = \vec{\boldsymbol{r}}_0 + \vec{\boldsymbol{v}}_0t + \frac{1}{2}\vec{\boldsymbol{a}}t^2.
\end{eqnarray} Como vemos, la posición de este movimiento tiene la misma ecuación que la obtenida para el MRU, ecuación (3), pero con un término extra que depende de $t^2$. Si analizamos ambas ecuaciones basándonos en su dependencia con el tiempo, la del MRU sería una recta, mientras que la del MRUA sería una parábola.

En cuanto a la velocidad, dado que la aceleración es constante, utilizando la ecuación (2)
se obtiene:
\begin{eqnarray}
\vec{\boldsymbol{a}} = \frac{d\vec{\boldsymbol{v}}}{dt} \ \rightarrow\ \ d\vec{\boldsymbol{v}} = \vec{\boldsymbol{a}} dt
\ \rightarrow\ \ \int_{\vec{v}_0}^{\vec{v}}d\vec{\boldsymbol{v}} = \int_0^t \vec{\boldsymbol{a}} dt \ \rightarrow\ \
\vec{\boldsymbol{v}} = \vec{\boldsymbol{v}}_0 + \vec{\boldsymbol{a}} t.
\end{eqnarray}
Nótese que esta ecuación se podría haber conseguido también, basándonos en la ecuación (1), derivando la ecuación de $\vec{\boldsymbol{r}}$ respecto del tiempo.

Movimiento circular uniforme
Lo que caracteriza a este movimiento es una trayectoria circular, y que en intervalos de tiempo iguales recorre ángulos iguales. Si llamamos $\theta$ al ángulo del vector posición $\vec{\boldsymbol{r}}$, tendremos la situación que muestra la figura.

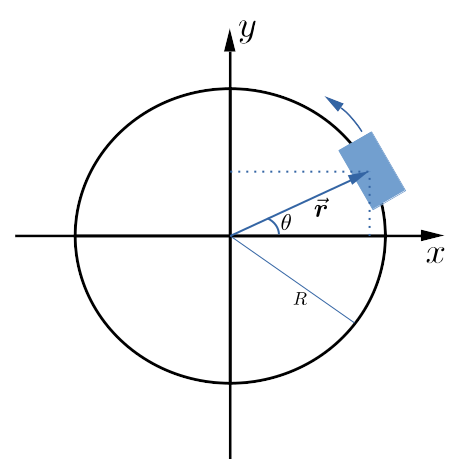
El rectángulo azul se encuentra haciendo un movimimiento circular uniforme.

La posición del cuerpo que hace el movimiento circular uniforme se puede obtener utilizando el seno y el coseno del ángulo $\theta$, obteniendo \begin{eqnarray}
x &=& R\cos\theta,
\nonumber\
y &=& R\sin\theta, \ \ \ \ \ (4)
\label{r_MCU}
\end{eqnarray} siendo $R$ el radio de la trayectoria circular. El vector de posición sería $\vec{\boldsymbol{r}} = (x,y)$. Teniendo la posición, sólo tendríamos que derivarla respecto del tiempo para obtener la velocidad. Pero $\vec{\boldsymbol{r}}$ no está escrita en función del tiempo y sabemos que el ángulo $\theta$ varía con el tiempo. Tendremos, por tanto, que determinar cómo es la dependencia del ángulo $\theta$ con el tiempo. En este movimiento, se define habitualmente una velocidad angular $\omega$ que nos dice cuánto ángulo avanza el móvil por unidad de tiempo. Esta cantidad se define como la cantidad de ángulo que avanza por unidad de tiempo, que en un momento dado será \begin{eqnarray}
\omega = \frac{d\theta}{dt}. \ \ \ \ \ (5)
\label{omega_def}
\end{eqnarray} que el móvil recorre ángulos iguales en tiempos iguales, la velocidad angular no variará en el tiempo, por lo que podemos deducir cómo es la dependencia de $\theta$ en función de $\omega$ \begin{eqnarray}
d\theta = \omega dt \ \rightarrow \ \int_{\theta_0}^{\theta} d\theta = \int_0^t \omega t \
\rightarrow \ \theta = \theta_0 + \omega t.
\end{eqnarray}Ahora ya se puede escribir la posición en función del tiempo, sustituyendo $\theta$ en las ecuaciones (4): \begin{eqnarray}
x &=& R\cos\left(\theta_0 + \omega t\right),
\nonumber\
y &=& R\sin\left(\theta_0 + \omega t\right)
\label{pos_MCU}
\end{eqnarray} y podemos derivarla respecto del tiempo para obtener la velocidad (ver ecuación (1)) \begin{eqnarray}
v_x &=& \frac{dx}{dt} = \frac{d\left(R\cos\left(\theta_0 + \omega t\right)\right)}{dt} =
-R\omega\sin\left(\theta_0 + \omega t\right) = -\omega y,
\nonumber\\
v_y &=& \frac{dy}{dt} = \frac{d\left(R\sin\left(\theta_0 + \omega t\right)\right)}{dt} =
R\omega\cos\left(\theta_0 + \omega t\right) = \omega x,
\end{eqnarray}en donde hemos utilizado las expresiones de $x$ e $y$ de la ecuación (4). Nótese que el vector velocidad queda entonces como \begin{eqnarray}
\vec{\boldsymbol{v}} = (- \omega y, \omega x) = \omega (-y, x).
\end{eqnarray}Lo primero que se puede deducir es que el vector $\vec{\boldsymbol{v}}$ es siempre perpendicular al vector de posición $\vec{\boldsymbol{r}} = (x,y)$, pues el producto escalar de ambos es nulo: \begin{eqnarray}
\vec{\boldsymbol{v}}\cdot \vec{\boldsymbol{r}} = \omega (-y, x) \cdot (x,y) = 0.
\end{eqnarray} Lo segundo, es que si calculamos el módulo de $\vec{\boldsymbol{v}}$ obtenemos \begin{eqnarray}
v = \omega \sqrt{y^2 + x^2} = \omega R,
\end{eqnarray} que relaciona el módulo de la velocidad con la velocidad angular.
Si volvemos a derivar la velocidad respecto del tiempo, se obtiene la aceleración del movimiento \begin{eqnarray}
a_x &=& \frac{dv_x}{dt} = \frac{d\left(-R\omega\sin\left(\theta_0 + \omega t\right)\right)}{dt} =
-R\omega^2\cos\left(\theta_0 + \omega t\right) = -\omega^2 x,
\nonumber\\
a_y &=& \frac{dv_y}{dt} = \frac{d\left(R\omega\cos\left(\theta_0 + \omega t\right)\right)}{dt} =
-R\omega^2\sin\left(\theta_0 + \omega t\right) = \omega^2 y,
\end{eqnarray} donde, de nuevo, hemos utilizado las ecuaciones (4). Así pues, el vector aceleración es \begin{eqnarray}
\vec{\boldsymbol{a}} = -\omega^2(x,y) = -\omega^2 \vec{\boldsymbol{r}}.
\end{eqnarray} Podemos ver que el vector de aceleración es paralelo al vector de posición pero de sentido contrario. es decir, siempre apunta hacia el centro de la circunferencia de la trayectoria. Dado que dicha dirección es siempre normal a la trayectoria del móvil, que es tangente a la circunferencia, a esta aceleración se le llama aceleración normal. Si escribimos el módulo de la aceleración, y lo hacemos en función de $v$ en lugar de $\omega$, se llega a la ecuación habitual de la aceleración normal: $a = v^2/R$.

Movimiento circular uniformemente acelerado
Para describir este movimiento conviene introducir una nueva cantidad que se denomina aceleración angular, y que viene dada por el cambio de velocidad angular con el tiempo \begin{eqnarray}
\alpha = \frac{d\omega}{dt}. \ \ \ \ \ (6)
\label{alpha_def}
\end{eqnarray}El movimiento circular uniformemente acelerado tiene como característica que el cuerpo que se mueve sigue una trayectoria circular, y que su aceleración angular es constante. Como en el caso del movimiento circular uniforme, la posición del cuerpo viene dada por \begin{eqnarray}
x &=& R\cos\theta,
\nonumber\
y &=& R\sin\theta,
\end{eqnarray} donde $R$ es el radio de la trayectoria circular y el ángulo $\theta$ va cambiando con el tiempo. Para saber cómo lo hace, calcularemos primero la velocidad angular a partir de la definición que hemos hecho de la aceleración angular en la ecuación (6): \begin{eqnarray}
\alpha = \frac{d\omega}{dt} \ \rightarrow \ d\omega = \alpha dt \ \rightarrow
\int_{\omega_0}^\omega d\omega = \int_0^t \alpha dt \ \rightarrow \ \omega = \omega_0 + \alpha t, \ \ \ \ \ (7)
\label{omega_MCUA}
\end{eqnarray} y ahora, utilizando la definición que hicimos de la velocidad angular, ecuación (5), podemos calcular el ángulo $\theta$ en función del tiempo \begin{eqnarray}
\omega = \frac{d\theta}{dt} \ \rightarrow \
d\theta = \omega dt \ \rightarrow \ d\theta = \left( \omega_0 + \alpha t\right) dt \ \rightarrow \
\int_{\theta_0}^\theta d\theta = \int_0^t\left( \omega_0 + \alpha t\right) dt \ \rightarrow \
\theta = \theta_0 + \omega_0 t + \frac{1}{2}\alpha t^2.
\end{eqnarray} Así pues, las componentes de la posición del cuerpo en el movimiento circular uniformemente acelerado son \begin{eqnarray}
x &=& R\cos\left(\theta_0 + \omega_0 t + \frac{1}{2}\alpha t^2\right),
\nonumber\\
y &=& R\sin\left(\theta_0 + \omega_0 t + \frac{1}{2}\alpha t^2\right). \ \ \ \ \ (8)
\label{x-y_MCUA}
\end{eqnarray} Ya tenemos la posición, $\vec{\boldsymbol{r}} = (x,y)$, por lo que solo tendremos que derivarla respecto del tiempo para obtener la velocidad \begin{eqnarray}
v_x &=& \frac{dx}{dt} = -R\left(\omega_0 + \alpha t\right)\sin\left(\theta_0 + \omega_0 t + \frac{1}{2}\alpha t^2\right)
= -\left(\omega_0 + \alpha t\right) y,
\nonumber\\
v_y &=& \frac{dy}{dt} = R\left(\omega_0 + \alpha t\right)\cos\left(\theta_0 + \omega_0 t + \frac{1}{2}\alpha t^2\right)
= \left(\omega_0 + \alpha t\right) x,
\end{eqnarray} donde hemos sustituido las componentes $x$ e $y$. El vector velocidad puede escribirse entonces como \begin{eqnarray}
\vec{\boldsymbol{v}} = \left(\omega_0 + \alpha t\right)(-y,x)
\end{eqnarray} que, como antes, es un vector perpendicular a la posición, pues el producto escalar $\vec{\boldsymbol{r}}\cdot \vec{\boldsymbol{v}}$ es nulo. Teniendo en cuenta la ecuación (7) de la velocidad angular, el módulo de la velocidad se puede escribir como \begin{eqnarray}
v = \omega\sqrt{y^2 + x^2} = \omega R,
\end{eqnarray} que nos da la relación entre la velocidad lineal y la angular. Si derivamos ahora la velocidad respecto del tiempo, obtenemos la aceleración \begin{eqnarray}
a_x &=& \frac{dv_x}{dt} = -R\left(\omega_0 + \alpha t\right)^2\cos\left(\theta_0 + \omega_0 t + \frac{1}{2}\alpha t^2\right) –
R\alpha\sin\left(\theta_0 + \omega_0 t + \frac{1}{2}\alpha t^2\right),
\nonumber\\
a_y &=& \frac{dv_y}{dt} = -R\left(\omega_0 + \alpha t\right)^2\sin\left(\theta_0 + \omega_0 t + \frac{1}{2}\alpha t^2\right) +
R \alpha\cos\left(\theta_0 + \omega_0 t + \frac{1}{2}\alpha t^2\right).
\end{eqnarray} Utilizando de nuevo la ecuación (7) de la velocidad angular, y las ecuaciones (8) de $x$ e $y$, la aceleración queda como sigue: \begin{eqnarray}
a_x &=& \frac{dv_x}{dt} = -\omega^2 x – \alpha y,
\nonumber\
a_y &=& \frac{dv_y}{dt} = -\omega^2y + \alpha x.
\end{eqnarray} Es decir, el vector aceleración se podrá escribir como\begin{eqnarray}
\vec{\boldsymbol{a}} &=& -\omega^2(x,y) + \alpha (-y,x).
\end{eqnarray}El primer término corresponde a la fuerza normal que ya vimos en el movimiento circular uniforme: es un vector dirigido hacia el centro del círculo, pues es paralelo a $(x,y)$ pero de sentido negativo. Si en lugar de escribirlo en función de $\omega$, lo escribimos en función de $v$, el modulo de esta aceleración será la expresión que habitualmente se enseña de la aceleración normal \begin{eqnarray}
a_n = \frac{v^2}{R}.
\end{eqnarray} El segundo término es perpendicular al vector de posición, y de hecho, es paralelo a la velocidad, pues ambos son proporcionales a $(-y,x)$ y con el mismo signo. Es la que se denomina aceleración tangencial. Su módulo será \begin{eqnarray}
a_t = \alpha\sqrt{y^2+x^2} = \alpha R.
\end{eqnarray}Nótese que la aceleración total se puede escribir entonces como \begin{eqnarray}
\vec{\boldsymbol{a}} = \vec{\boldsymbol{a}}_n + \vec{\boldsymbol{a}}_t,
\end{eqnarray}y como la aceleración normal y la tangencial son vectores perpendiculares, su módulo será \begin{eqnarray}
a = \sqrt{a_n^2 + a_t^2}.
\end{eqnarray}

Conclusión
Si habéis llegado hasta aquí y no habéis hecho todos los cálculos (algo comprensible, porque te tiene que pillar con ganas, boli y papel), siempre podréis regresar para completar vuestra iniciación cinemática cuando mejor os convenga. Y si habéis hecho los cálculos, cuando os enfrentéis a cualquier criatura cinemática, en lugar de decir ‘huid insensatos’, ahora podréis decir con tranquilidad ‘cuenta con mis dos ecuaciones’.

PD: por si alguien se ha perdido con algunas referencias, corresponden a las películas de El Señor de los Anillos.

Autor: Adolfo Vázquez Quesada.

Adolfo Vázquez Quesada es profesor del Departamento de Física Fundamental de la UNED.