Autores: Jaime Arturo de la Torre, Pep Español.
Imagina que sostienes un ladrillo en la mano, lo alzas y luego lo lanzas al aire. A simple vista, parece un movimiento trivial: sube, se detiene un instante y baja. Sin embargo, si observas con atención descubrirás una danza mucho más compleja, donde intervienen rotaciones inesperadas, giros abruptos y fenómenos que desafían la intuición. ¿Cómo se puede describir matemáticamente toda esta complejidad?
Esa pregunta se la planteó Leonhard Euler (1707–1783), uno de los matemáticos más prolíficos de la historia quien, entre sus enormes aportaciones, formuló las ecuaciones que hoy llevan su nombre y que describen la dinámica de un cuerpo rígido girando en el espacio. Según estas ecuaciones, si el ladrillo fuera perfectamente esférico, cualquier eje de rotación sería equivalente; pero un ladrillo tiene tres ejes principales — longitudinal, transversal y vertical — cada uno con un momento de inercia distinto. Un eje principal es aquel alrededor del cual el cuerpo gira «más fácilmente». Cuando el ladrillo gira ya sea sobre el eje de momento de inercia mayor o el de momento de inercia menor, permanece girando indefinidamente alrededor de dichos ejes en una rotación «pura». Sin embargo, cuando gira alrededor del eje que tiene momento de inercia intermedio, la cosa se pone interesante: cualquier pequeña perturbación «saca del eje» al ladrillo que, repentinamente da un giro inesperado. Las ecuaciones de Euler predicen que la rotación alrededor del eje intermedio es inestable: al principio el ladrillo gira «tranquilamente», pero pequeños desvíos crecen exponencialmente y terminan por voltearlo de golpe.
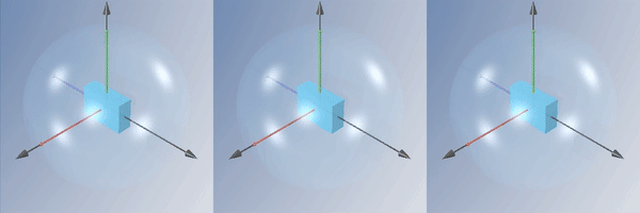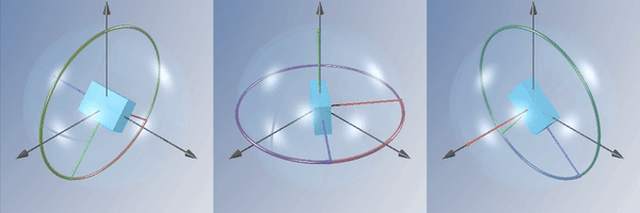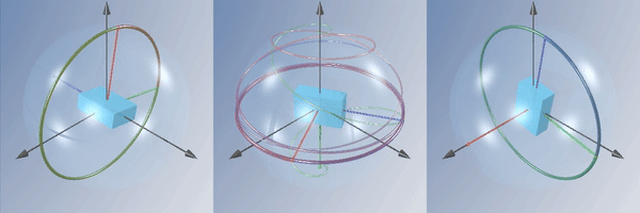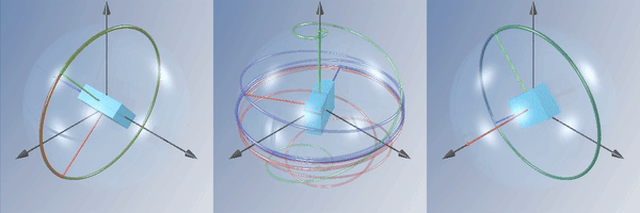
En la práctica puedes observar este efecto de la siguiente manera: si agarras una raqueta de tenis por el mango y la lanzas girando alrededor del eje que une el centro de las cuerdas con el mango (el eje intermedio), verás que en algún punto de su trayectoria la raqueta de pronto gira 180° inesperadamente. Esto es justamente la inestabilidad del eje intermedio.
El mismo fenómeno, en un contexto completamente distinto fue observado por el cosmonauta soviético Vladimir Dzhanibekov (de apellido a veces transliterado “Janibekov”). Estaba a bordo de la estación Salyut 7 en 1985 cuando observó en gravedad casi cero que una pequeña llave en forma de T lanzada al aire giraba con dos rotaciones estables y una repentina inversión respecto al eje intermedio. La sorprendente claridad de la maniobra en microgravedad cautivó a la comunidad científica y popularizó el “efecto Dzhanibekov”.
Como se aprecia en el video, parece que la llave permanece cambiando su sentido de giro indefinidamente. Sin embargo, en el mundo real, nada es perfectamente rígido ni está libre de rozamientos. El aire, por ejemplo, puede generar una fricción que llegue a parar la llave. Lo más sorprendente es que incluso en ausencia de aire, la llave terminará dejando de cambiar su sentido: en efecto, la estructura atómica del cuerpo, con su incesante agitación térmica, es responsable de que la energía acumulada en una forma de rotación se vaya transfiriendo — en forma de calor — a otros grados de libertad del sistema. La consecuencia de toda esta disipación intrínseca es que el objeto dejará de girar inestablemente alrededor del eje intermedio, para girar establemente alrededor el eje que le resulta «más fácil», el que tiene momento de inercia mayor. Dicho de otro modo: la disipación destruye la inestabilidad, y la inversión brusca del ladrillo deja de ocurrir.
Nos podemos preguntar entonces cómo son las ecuaciones que gobiernan el movimiento de un sólido real que siendo casi rígido necesariamente tiene que describir la capacidad de redistribuir la energía entre sus formas de movimiento. Nuestro grupo de la UNED se ha hecho también esta pregunta y la ha resuelto satisfactoriamente en una serie de trabajos, escribiendo las ecuaciones que generalizan las centenarias ecuaciones de Euler y describe cómo se produce esta transferencia de energía [1,2,3]. Cuando hay disipación, esto es lo que hace el cuerpo:
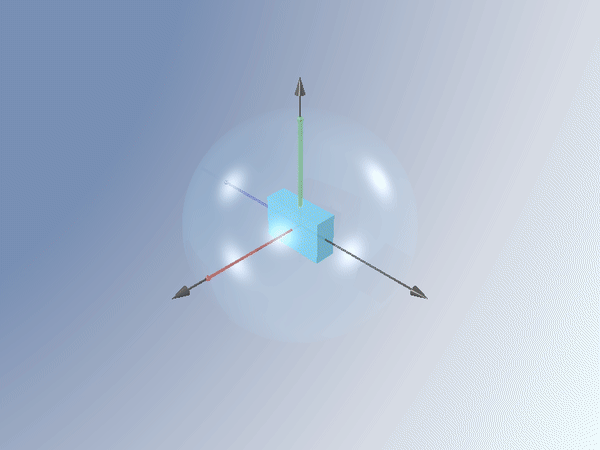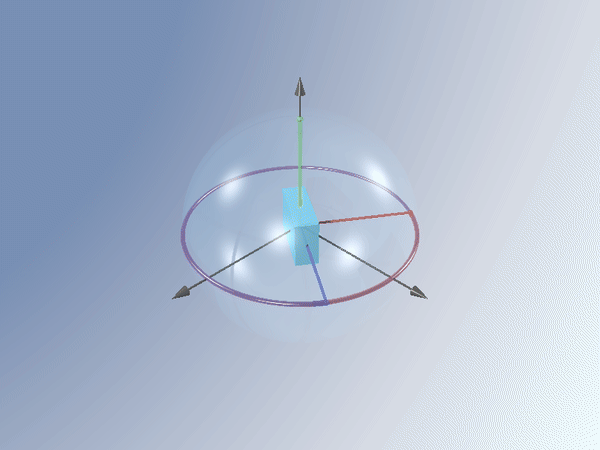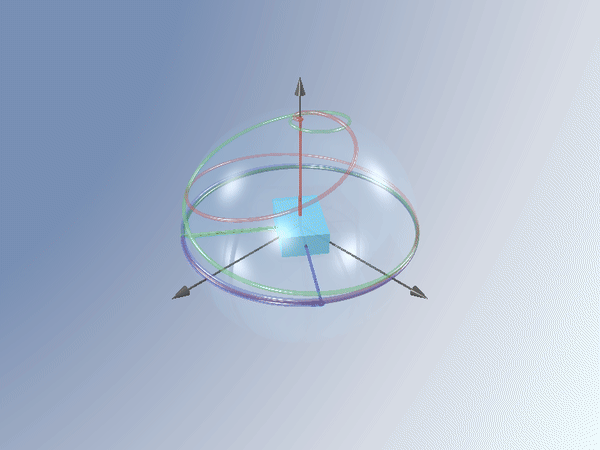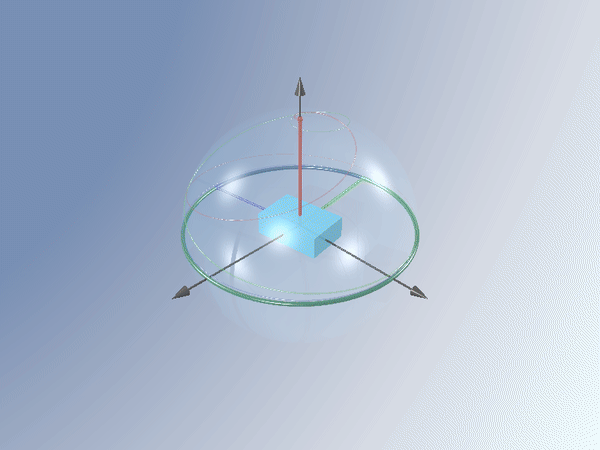
Lo más sorprendente de esta transición de girar (inestablemente) alrededor del eje intermedio a girar (establemente) alrededor del eje mayor es que el sólido ¡se calienta!. En efecto, la energía total se conserva, pero la energía cinética de rotación alrededor del eje intermedio es mayor que la correspondiente al eje mayor, en la transición del giro alrededor de un eje a otro, esa diferencia de energía se invierte en calentar el cuerpo.
Es fascinante ver cómo un simple giro inestable — ese vuelco repentino alrededor del eje intermedio– predicho por la mecánica clásica revela la mano oculta de la termodinámica a través de la posterior disipación de esa misma energía rotacional en forma de calor. En un mismo experimento convergen la elegancia de las ecuaciones de Euler y el principio de conservación de la energía, cuya “pérdida” aparece como un aumento de temperatura.
Y aquí va una pregunta interesante: Imagina que haces girar una moneda sobre uno de sus diámetros en el espacio exterior. De acuerdo con este efecto disipativo, la moneda terminará girando sobre su eje de simetría axial, poniéndose plana. ¿Puedes estimar cuánto se calienta la moneda en este proceso?
Autores: Jaime Arturo de la Torre, Pep Español
Jaime Arturo de la Torre y Pep Español son profesores del Departamento de Física Fundamental de la UNED.
[1] Stochastic dissipative Euler’s equations for a free body, de la Torre, Jaime Arturo, Sánchez-Rodríguez, Jesús and Español, Pep. Journal of Non-Equilibrium Thermodynamics. https://doi.org/10.1515/jnet-2024-0029 (2024)
[2] Internal dissipation in the Dzhanibekov effect, J.A. de la Torre; Pep Español, European Journal of Mechanics – A/Solids 105298 (2024)
[3] The role of thermal fluctuations in the motion of a free body, Pep Español, Mark Thachuk, J A de la Torre, European Journal of Mechanics – A/Solids, Volume: 103, Pages: 105184-105184. (2024) 10.1016/j.euromechsol.2023.105184